


|
6.10 Location of a "supporting facility" Consider the network of Figure P6.10 and imagine that the nodes represent five cities, the numbers next to the nodes the "weights" of the cities, and the numbers next to the links the mile length of roadways connecting the cities. Cars travel on the roadways at an effective speed of 30 mph. Assume that a major facility, say an airport, has been located at some point on this network. A regional planning group now wishes to install a high-speed transportation link to the airport with a single station. The high-speed vehicles will travel on the network at twice the speed of cars and their route will be the shortest route to the airport. It is assumed that travelers to the airport will choose that combination of transportation modes which minimizes their access time to the airport (ignoring transfer times). To clarify the description above, assume that the airport is at node 2
and that the single station of the high-speed link is located at node 5.
Then, the access time to the airport of travelers from node 5 is 25 minutes.
However, the access time of
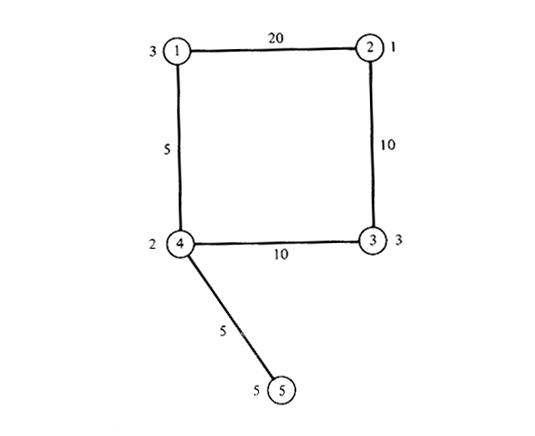
travelers from node 1 is still 40 minutes. at would take travelers from node 1 exactly 20 minutes to get to node 5 by car and then another 25 minutes to get from 5 to 2, so that it is better to go directly to the airport by car.)
It can be shown that the result you proved in part (a) holds as long as the functions f[d(x, y)] and g[d(x, y)] are both concave in d(x, y) [MIRC 79a]. |