|
6.17 Facility location with queueing Consider two small
towns which are one unit distance apart, as shown in Figure P6.17.
(Each town is represented as a single point (node) on this simple "network,"
i.e., intra-town distances can be considered insignificant).
A hospital equipped with a single ambulance is located at some point
between the two towns which is a distance x away from the halfway point
between the two towns.
Calls from the two towns that require dispatching of the ambulance occur
in a Poisson manner at a combined rate 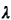 = 1/4 calls/unit time. A
fraction fA of these calls come from Town A and a fraction
fBfrom Town B (fA + fB = 1) = 1/4 calls/unit time. A
fraction fA of these calls come from Town A and a fraction
fBfrom Town B (fA + fB = 1)
In responding to each call the ambulance travels to the appropriate city
at a constant speed v, spends a constant amount of time 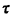 on the scene
(picking up a patient) and returns to the hospital (with the patient) at the
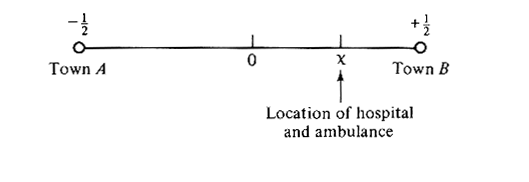
same constant speed v. Let v = 1 distance unit/time unit and on the scene
(picking up a patient) and returns to the hospital (with the patient) at the
same constant speed v. Let v = 1 distance unit/time unit and 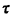 = 1 time unit. = 1 time unit.
Calls for ambulance dispatching queue up in a first-come, first-served
manner until the ambulance eventually serves them. We define the "total
response time" of the ambulance to a patient as the time interval between
the instant when that patient calls for the ambulance and the instant when
the patient arrives at the hospital.
| a. | Assuming steady-state conditions,
find the expected total response time to a random patient. Your answer
should be in terms of x, fa and fb only.
Hint: To keep the algebra simple, write your answer in terms of
x and of (fa - fb).
| | b. | If the objective is to minimize the
expected total response time per patient, what is the optimal value of
x when fa = fb = 1/2?
| | c. | Does your answer in (b) agree with or
violate Hakimi's theorem for the location of a median on networks?
Please explain briefly.
| | d. | In the general case
(arbitrary 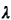 , , 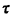 , v, fa and fb), does the question of
whether steady-state is reached depend on the location of the
hospital/ambulance? Please explain briefly (no mathematics).
, v, fa and fb), does the question of
whether steady-state is reached depend on the location of the
hospital/ambulance? Please explain briefly (no mathematics).
| | e. | Suppose now that all calls that find
the ambulance busy, i.e. away from the hospital, are lost (e.g., the
patients are transported to the hospital by taxi). Where should the hospital
be located in this case if fa = 0.8 and fb = 0.2
(and, as before, 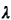 = 1/4, = 1/4,
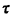 = 1, v = 1) and the objective is still to
minimize expected total response time for those patients who are served
by ambulance? (Note that no queueing ever occurs in this case.) = 1, v = 1) and the objective is still to
minimize expected total response time for those patients who are served
by ambulance? (Note that no queueing ever occurs in this case.)
| | f. | Repeat part (e) assuming that an
additional constraint is that no total response time should ever exceed
2.6 units (induding the time on the scene).
|
|


