6.8 Coin collection from parking meters Figure P6.8 shows a section of a downtown area. A special coin-collection truck must traverse all street segments indicated with solid lines once a week, to collect coins deposited in parking meters by motorists. Parking meters exist on only one side of these streets.

Street segments indicated by dashed lines do not have parking meters and therefore need not be traversed, except as necessary to travel between parts of the downtown street grid.

Travel in all street segments is permitted in only one direction, as indicated by the arrows in Figure P6.8. An east-west block is 9 units long, and a north-south block is 6. Diagonal street segments are 11 units long. Note that there is no direct connection between points 3 and 7.

What is the length of the shortest route that the truck can travel beginning and ending at point 1 and traversing, at least once, all street segments with parking meters? Describe one such shortest route.

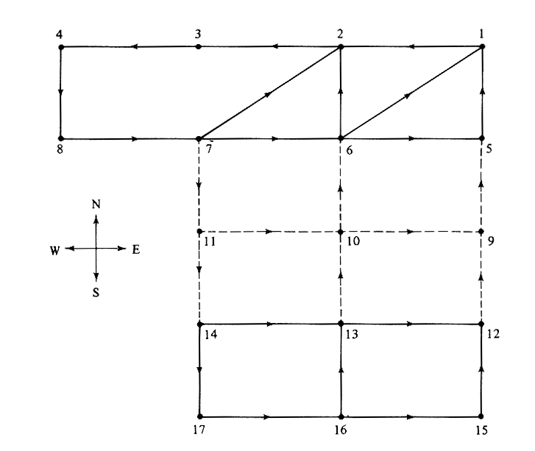
How is this problem different from the CPP on directed networks? Can you devise a systematic procedure for dealing with this family of problems ?