


7.2.1 Efficient Sorting and SearchingIn simulating urban systems it is often necessary to sort long arrays of numbers such as the coordinates of incidents, the addresses of mail recipients, or the times at which requests for service occurred. Equally important, sorting algorithms play a central role as "building blocks" in techniques aimed at resolving several important geometrical problems, as we shall see shortly. It is therefore important to develop a sorting algorithm that is as efficient as possible. Suppose that we are given n integers and that we wish to sort them in,
say, increasing order of magnitude with the smallest number at the top
of the list. The straightforward approach is to scan the initial list of
numbers in order to find the smallest of them; this requires n - I
comparisons. We make this smallest number the first element of our
sorted array. We then scan the list of the remaining n - I numbers for
the second smallest number in the initial list (thus performing n - 2
comparisons) and continue in this manner until all the numbers are
sorted. This is, then, a 0(n2) algorithm, since the
total number of comparisons required is
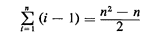
A more subtle approach, however, leads to an algorithm which is 0(n· log2 n). This approach is illustrated in Figure 7.13 for an array of 16 numbers involving the integers I through 16. 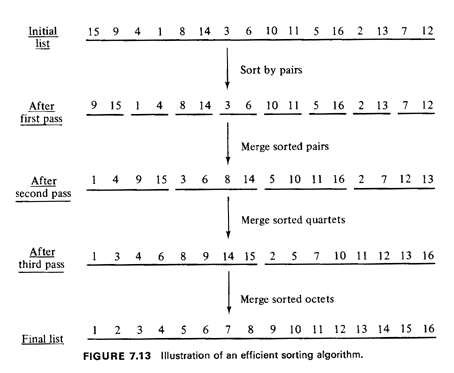
To describe this approach, let us assume, at first, that it so happens that n = 2k, where k (= log2 n) is a positive integer. The algorithm then begins by forming a sorted pair of numbers after comparing the first and the second numbers in the initial list, a second sorted pair from the third and the fourth numbers, a third pair from the fifth and the sixth, and so on–see second row of Figure 7.13. The algorithm then goes through k - 1 more merging passes over the list, forming in the process sorted sublists of numbers, first, with four members, then with eight, then with sixteen, until finally, the whole list of numbers is fully sorted. The key observation that leads to the algorithm is that the merging of two previously sorted lists of length m requires at most 2m - 1 comparisons [i.e., this type of merging is a 0(m) procedure]. Omitting the details, it is clear that since there are O(n) comparisons on each pass through the list of numbers and since there are k passes until the list is completely sorted (e.g., for n = 16 there are log, 16 = 4 passes), the algorithm is 0(nk) = O(n -log2 n). Exercise 7.4 Show in detail that the algorithm described above is 0(n. log2 n). What if the length of the list of numbers to be sorted, n, is not a power of 2? Let then k = [log, n] (where again the notation [a] stands for "the smallest integer that is greater than or equal to a"). We may then add 2k - n very large numbers to our initial list. After the expanded list has been sorted, its first n elements will constitute a sorted list of the original n numbers. The time required by our algorithm to sort the expanded list is O(k.2 k) , and since n is of the same order as 2 k and log, n differs from k by less than 1 unit, this is equivalent to O(n log, n). The technique outlined above, which is typical of a common approach to many combinatorial problems, is often referred to as "divide and conquer." The idea, of course, is to solve the problem in small parts (e.g., by sorting initially only pairs of numbers as we did in the algorithm described above) and then to combine these parts in an efficient manner to arrive at the solution of the whole problem. Another example of this approach solves efficiently the problem of adding a new number (at its proper place on the list) to an already sorted list of n numbers. By determining, first, whether the new number should be in the upper or lower half of the list [this can be done by comparing the new number with the (n/2)th element in the list], then the quarter in which it falls, and so on, this problem can be answered in O(log2 n) time. Note that this procedure is equivalent to one that we would have followed if we were searching for a specific number on the list. Therefore, the procedure is known as an efficient algorithm for searching through a sorted list and, as we just saw, it is O(log2 n). |