7.3 Poisson demands with time-dependent rate, revisited We have already seen a procedure for simulating the generation of demands in an urban service system according to a Poisson process with time-dependent mean rate 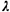(t) That procedure (Section 7.1.4) required two "passes" over the interval [0, 71: once to determine the number of demands during [0, T] and a second time to generate the time instants when these demands occur. In this problem you will be asked to develop an alternative procedure which requires only a single pass.

Refer once more to Figure 7.12. Define a function 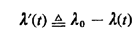'(t) such that



where 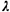0 is the maximum value of 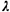(t) in [0, T].

Suppose now that we used ti = (-n ri)/ 0 to generate sample values of successive demand interarrival times, beginning at t = 0. This, of course, would lead to too many demands being generated in [0, T]. (The expected number of demands would be equal to 0 ยท T.)

How would you modify the foregoing procedure (by accepting or rejecting some demands) using (t) and '(t) to make it work correctly?