


7.7 Simulating Buffon's needle experiment 11 Recall Buffon's needle
experiment, the famous early experiment involving geometrical
probability concepts, from Section 3.3. 1. Assuming that the length of
the needle, 1, does not exceed the spacing, d, between parallel lines (I
 d), the probability that a randomly thrown needle intersects a line
was shown to be d), the probability that a randomly thrown needle intersects a line
was shown to be
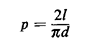
Thus, by conducting Buffon's experiment many times, one can obtain an estimate for 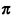 , say , say 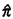 ,
through ,
through
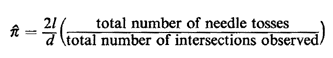
Suppose that we wish to perform these experiments by using computer simulation. After all, it may take a large amount of time to toss a needle, say, a few thousand times, although this has not been sufficient to discourage several people in the past from doing just that (up to 10,000 consecutive tosses have been reported). Consider the following three alternative methods for simulating Buffon's needle experiment. (For each execution of the experiment, new random numbers must be drawn.) Method 1 1. Obtain a random value for X, say x, from the uniform distribution on the interval [0, d] (i.e., x = r1d). 2. Obtain a random value for S, say s, the sine of the angle which the needle forms with the set of parallel lines (see Figure 3.17) from the uniform distribution on [0, 1] (i.e., s = r2). 3. if x Method 2 1. Obtain a random value y1 for Y1, from the uniform distribution on the interval [0, d/2] (i.e., y1 = r1d/2). Let (0, y1) represent the midpoint of the needle. 2. Obtain a random value, x2, for X2, from the uniform distribution on the interval [-l/2, +l/2] (i.e., X2 = r2l - 1/2). 3. Similarly, obtain a random value, y2, for Y2, using y2 = r3l - l/2. [(x2, y2 + y1) will be the coordinates of some point lying on the needle.] 4. If (x22 + y22)1/2
5. if
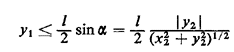
an intersection has occurred. Method 3 1. Obtain a random value, x1, for X1 from the uniform distribution on the interval (0, d] (i.e., x1 = r1d). 2. Similarly, obtain a random value, y1, for Y1, using y1 = r2d. Let (x1, y1) represent the midpoint of the needle. 3. Similarly, obtain random values (x2, y2), for (X2, Y2) using x2 = r3d and y2 = r4d. 4. Let the end points of the needle lie on the line joining (x1, y1) with (x2, y2) at a distance 1/2 from (x1, y1) in each direction. 5. If y1 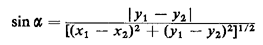
an intersection has occurred. a. Provide a physical interpretation of each one of the three methods by drawing figures that show schematically what each method does. b. Which of the foregoing three methods are correct, which are incorrect, and why? Hint: Two of the methods are incorrect. |