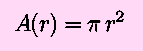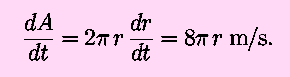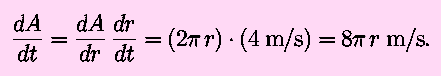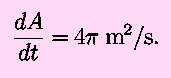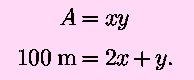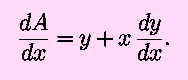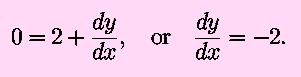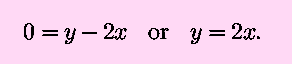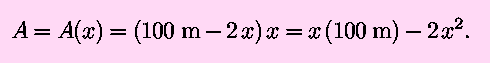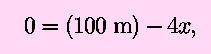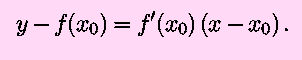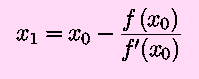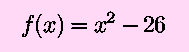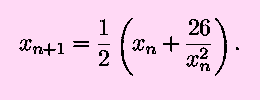Unit 5: More Applications of Differentiation

The next application of the derivative is related rates. The usual problem here is to have a function, say the area of a circle of radius r,

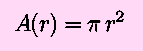and a derivative, such as dr/dt=4 m/s, and we wish to find another derivative, in this case dA/dt. In other words, to relate the unknown rate to the known rate. There are two basic methods, which are roughly equivalent:
  1. Use implicit differentiation. In this case, differentiate with respect to time:

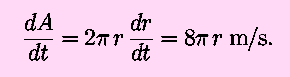
  2. Use the chain rule:

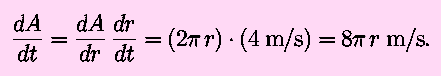
Note that in both cases we need to know the current value of the radius to specify the change in the area. When r=0.5 m,

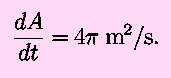Note that these problems can get tricky, either because of a large number of derivatives floating about, or because of difficulty in setting up the geometry of the situation. Also note that in this case, the units of the answer are what they should be.

Next, we have max-min problems. The basic situation here is that we have several quantities related to each other by various formulae. We wish to either minimize or maximize one of the quantities by appropriate choices for the values of the others. Recall that, in a smooth region, the maxima and minima occur when the first derivative is zero. So our method is to set up a derivative, set the expression for the derivative equal to zero and solve, and then ``solve backwards'' to get the desired values. A typical example is the case of a farmer who lives next to a straight stream. He has bought 100 m of fence and wishes to enclose as much pasture as possible, using the stream as one side of the pasture. He also insists that the pasture be rectangular. To set this up, we call the length of the side opposite (or parallel to) the stream y, the common length of each one of the sides adjacent to the river x, the area A and obtain

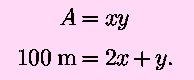At this point, we could choose either x or y to be the variable for which we solve. For consistency with previous usage, we will solve for y as a function of x.

We could eliminate either variable in favor of the other; that will be done later, as a check. Using implicit differentiation, differentiate the first of the above equations with respect to x to obtain

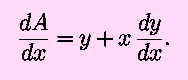Differentiate the second equation to obtain

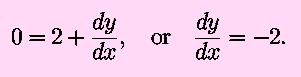Setting dA/dx=0 and subsituting dy/dx=-2,

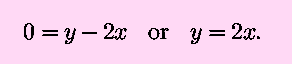Subsituting into the second of the first set of equations (sometimes known as ``Solving backwards'') gives x=25 m, y=50 m, and A=1250 m².

How do we know this is the maximum, and not a minimum? Well, it's fairly obvious in a simple example like this, but in general:

  1. Check near the supposed maximum; x=24 m, y=52 m gives A=1248 m² and x=26 m, y=58 m gives A=1248 m². Both are smaller than the solution, so we're okay. (By the way, it is not a coincidence that changing the value of x by the same amount either way gives the same area.)
  2. Check borderline cases or discontinuities. Here, x=0, y=100 m and x=50 m, y=0 both give A=0.
  3. Use common sense. Don't let lengths, areas or volumes go negative. We found only one extreme, and that can't be a minimum, as that would mean there is no maximum.

The trick to max-min problems is setting things up so that when you solve for the derivative equal to zero, you actually have an equation you are capable of solving.

To check, as promised, substitute y=100 m-2x into the original expression for the area to obtain

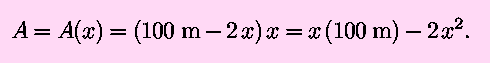Differentiating with respect to x and setting the derivative equal to zero gives

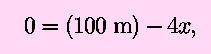which is readily solved for x=25 m, as before.
As another use of differentiation for this unit, we present Newton's method for approximating roots of equations. This section is completely optional. The idea is as follows: we have an equation f(x)=0, and wish to solve for a value of x. We start with a guess, x0, and try to improve the guess. At the point (x0, f(x0)), the tangent to the curve is given by the equation

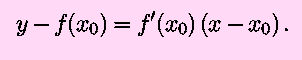We solve this to find the point where the tangent line crosses the x-axis, where y=0. Denoting this value of x as x0,

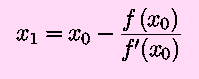x1 = x0 - (f(x0) / f'(0))
The above procedure is indicated by considering a figure of the curve of a typical function:

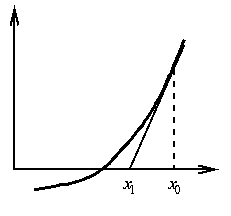If we started somewhere near the desired root, and f(x) is well-behaved (we'll leave ``well-behaved'' ill-defined for the moment), then x1 will be closer to the root than x0. We continue the process, calculating x2, x3, etc., until we are near enough to the root to be satisfied. (``Near enough'' is commonly defined in terms of the number of digits of accuracy possessed by the calculator or computer in use, or given in a particular problem at hand.)

For an example that is easily checked, consider

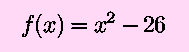which leads to, with an extension of the notation,

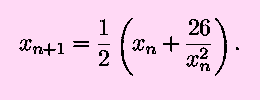that is, we wish to find the square root of 26. Of course, any calculator that could perform the calculations necessary to use Newton's Method will be able to find the square root immediately. This is for demonstration purposes only.

Starting with x0=5 gives x1=5.1 (this first step might even be done without a calculator). Then, x2=5.00990196. To this same precision, the square root of 26 is 5.00990195. Note that this took only two iterations. When Newton's method works, it works fairly well. For finding things like roots to quadratics and cubics, the number of correct digits in the answer roughly doubles at each step. For finding roots of functions more complicated than polynomials, Newton's method is less reliable. The text shows examples where Newton's method fails entirely.

Objectives:

You should understand what the Mean Value Theorem says; don't worry excessively about its proof. You should be able to find values for indeterminant forms, using L'Hopital's Rule where appropriate.

Suggested Procedure:

Independent Study page | Calculus page World Web Math Categories Page

watko@mit.edu
Last modified August 1, 1998