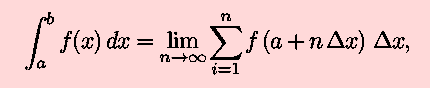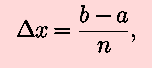Unit 8: Geometric Applications of the Integral

We consider in this unit several things that can be done with the definite integral. In unit 7, we defined

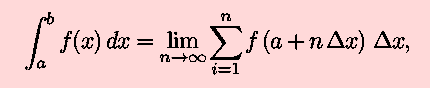where

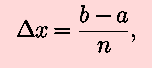as a way of calculating the area under a curve. We now extend this idea to using integrals for other geometric purposes. In each case, we show the quantity to be calculated can be approximated by a sum of ``slices'' of one form or another. We then take a limit process to reach infinitely many thin slices, which will be an integral.

Objectives

After completing this unit you should be able to set up integrals to calculate areas, areas between curves, volumes of solids of revolutions (by both disk and shell method), arc lengths, and areas of surfaces of revolution.

Suggested Procedure

  1. Simmons 7.1-7.6
  2. Work many of the problems at the ends of each section. Be sure that you are capable of setting up the integral for any of the geometric problems presented. The ability to solve such integrals is also important, with the caveat that you haven't been given all of the techniques of integration yet. Still, the problems are mostly designed so as to produce an integral you can solve.
  3. Take the Practice Test, Xdvi or PDF.
Independent Study page | Calculus page World Web Math top page
watko@mit.edu
Last modified August 1, 1998