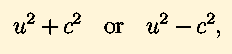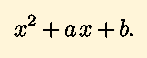Unit 9: Methods of Integration

The main thrust of this unit will be to give a list of substitutions that would otherwise probably not occur to you. Specifically, we have the trigonometric substitutions, where we replace an expression involving a square root with an expression full of cosines and tangents. It would seem that we leap from the frying pan into the fire, but we are saved by the fact that there are lots of ``cute'' things to be done to trigonometric integrals. Pay special attention to the half-angle identities, which are often used to reduce the exponents of sines and cosines down to something reasonable.

To complement our fun with trigonometry, we pull another trick out of high school mathematics and resurrect completing the square. We need this since most of our formulas are designed for expressions containing

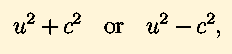as opposed to the more general

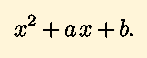So, we complete the square to have the neccesary portions of the integrands appear in the proper form.

This presentation is deliberately short on details; said details are all in the texts.

Objectives:

After completing this unit you should be able to integrate many more functions than before. In fact, you should be able to integrate any of the common integratable functions.

Suggested Procedure:

  1. Read Simmons Chapter 10
  2. Sorry, there are not yet any World Web math entires on this topic.
  3. Clearly, you are going to need to work lots of problems if you are going to have any hope of remembering the dozen or so tricks presented in this unit. Again, no problems are inherently better than others, so work a nice variety.
  4. Take the Practice Test, Xdvi or PDF.
  5. Ask your instructor for a unit test.
Independent Study page | Calculus page World Web Math Categories Page
watko@mit.edu
Last modified August 1, 1998