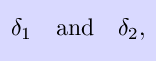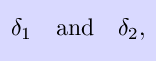The Squeeze Theorem
The Squeeze Theorem
Suggested Prerequesites:
Formal look at limits
Our immediate motivation for the squeeze theorem is to so that we can
evaluate the following limits, which are necessary in determining the
derivatives of sin
and cosine:
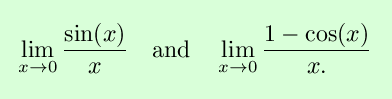
The squeeze theorem is applied to these very useful limits on the page
Useful Trig Limits.
The Squeeze Theorem:
If there exists a positive number p with the property that

for all x that satisfy the inequalities


then
Proof (nonrigorous):
This statement is sometimes called the ``squeeze theorem'' because it
says that a function ``squeezed'' between two functions approaching
the same limit L must also approach L.
 Intuitively, this means that the function
f(x) gets squeezed between the other
functions. Since g(x) and h(x)
are equal at x = a, it must also be
the case that
f(x)=f(x)=L
since there is no room for x to be anything else.
Intuitively, this means that the function
f(x) gets squeezed between the other
functions. Since g(x) and h(x)
are equal at x = a, it must also be
the case that
f(x)=f(x)=L
since there is no room for x to be anything else.
For the formal proof, let epsilon be given, and chose
positive numbers
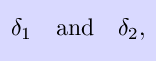
both less than p, so that

Define 
to be the smallest of the numbers
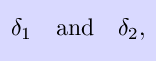
Then

implies


and the proof is complete.
The Squeeze Theorem applied to Trig Limits |
Back to the Calculus page
Back to the World Web Math top page
watko@mit.edu
Last modified October 9, 2001
 The Squeeze Theorem
The Squeeze Theorem The Squeeze Theorem
The Squeeze Theorem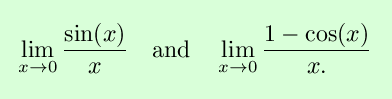




 Intuitively, this means that the function
f(x) gets squeezed between the other
functions. Since g(x) and h(x)
are equal at x = a, it must also be
the case that
f(x)=f(x)=L
since there is no room for x to be anything else.
Intuitively, this means that the function
f(x) gets squeezed between the other
functions. Since g(x) and h(x)
are equal at x = a, it must also be
the case that
f(x)=f(x)=L
since there is no room for x to be anything else.