Cartesian Coordinate Exercise Solutions

1. Right handed axis system

   
   (The positive y-axis points into the page.)

   Left handed axis system

   
   (The positive y-axis points into the page.)

2. The cartesian coordinates of the origin are (0, 0, 0). The cartesian coordinates of a point on the x axis would have the form (x, 0, 0) for some x. The coordinates of a point on the plane containing the y and z axes would look like (0,  y, z).

3. Answer

   

4. The Three-Dimensional Pythagorean theorem

   If a point P has coordinates (x₁, x₂, x₃), then its distance from the origin is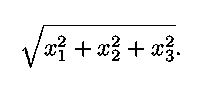
   

   Proof: Project the point P onto the x-y plane and call this projection P'. Project P' onto the x axis and call this projection P''. Now we have two right triangles to consider:

   

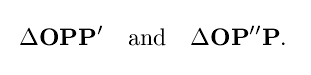
   Let's consider the second of these first. Now, the leg of this triangle from the origin O to the point P'' has length |x₁| and the leg from P' to P'' has length |x₂|, so by the normal (two-dimensional) Pythagorean theorem, the hypotenuse of this triangle, which is the length of the segment from the orign to P', is

   

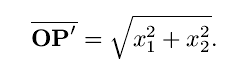
   But the segment from P' to P has length |x₃|, so by applying the Pythagorean theorem once again, we get that

   

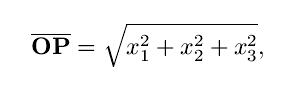
   as desired.