N-Tuples

The set of all N-tuples is refered to as R^N, where the R stands for ``Real Number''. [You could also talk about Q<sup>N</sup>, the set of N-tuples of rational numbers (``Quotients''), or Z^N the set of N-tuples of integers (``Zahlen'' means ``Integer'' in German).] In these pages, we will be working mostly with R¹ = R, R²  and R³.

Tuples are useful whenever you want to gather a set of data together and consider it as a single unit. You might want to combine the result of a measurement with the time the measurement was taken into a pair, or combine all the 30 answers to a question in a psychological profile into a 30-tuple.

It is really easy to do arithmetic with tuples of the same size: you just do the operation on the first components of both tuples to get the first component of the answer, then repeat on the second componenets, etc. For example, if I sold 3 apples and 4 oranges on Monday, and 2 apples and 7 oranges on Tuesday, I could calculate my combined sales by adding the two 2-tuples: (3, 4) + (2, 7) = (5, 11). This is called component-wise addition.

One can also operate on a tuple by a single real number. To convert a 5-tuple of temperatures measured in Celsius to a 5-tuple of temperatures measured in Kelvin, I might want to add 273.15 to each component:

Similarly, to find the average of three triplets, I would add them up component-wise and then divide by three:

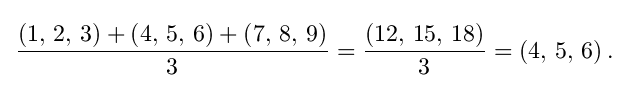
All by themselves, tuples may not represent a great deal of mathematical interest. Soon, however, we will use tuples to represent more interesting objects: points and vectors.

Exercises:

1. What is the fourth component of
   (31, 28, 31, 30, 31, 30, 31,  31, 30, 31, 30, 31)?

2. Calculate
   (1, 2, 3) - (4, 8, 2)

   using component-wise subtraction.