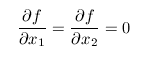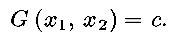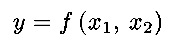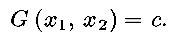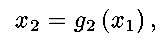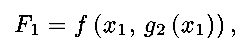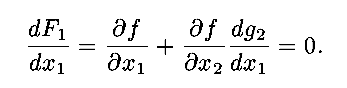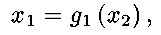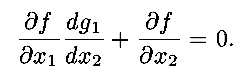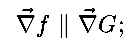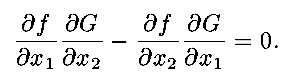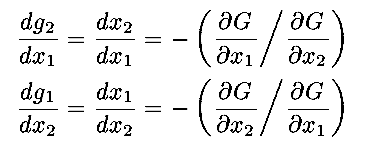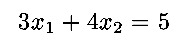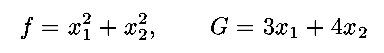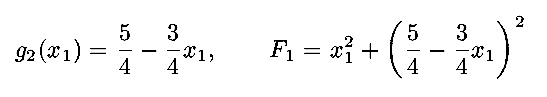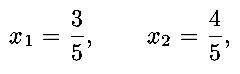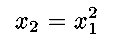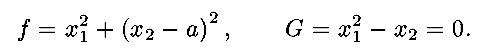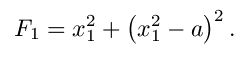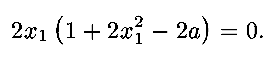Constrained Min/Max
Constrained Min/Max
This page is temporarily under construction
If you were hiking to the top of a hill, and looked out from the top,
you would know that you were at a relative maximum of altitude.
Indeed, if you had brought a coordinate system with you, or a compass
to identify the East and North directions, you would see that if the
altitude is represented as
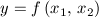 , then
, then
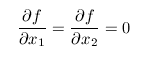
at this point. You might also convince yourself that
the second partials obey the condition for a maximum.
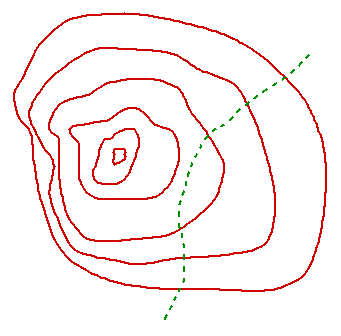
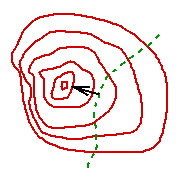
Suppose, however, that instead of going to the top, your path veers
away from the summit, as in the contour map below. In his map, the
dotted green curve is the path and the solid red curves are the
contours of constant elevation.
Suppose that the green curve is described by
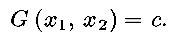
Then the highest point reached while
hiking along the path is the maximum of
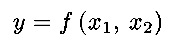
subject to the
constraint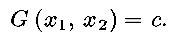
There are many ways to find this maximum height. One direct way is
to assume that the path may be described by one variable as an
explicit function of the other,
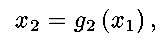
so that
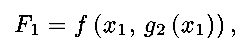
a function of a single variable. Then, differentiating and setting
equal to zero, using the chain rule gives
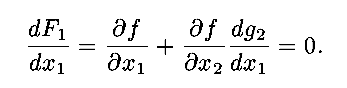
Similarly, if
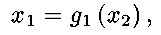
then the condition for an extreme is
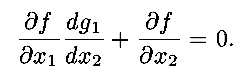
Imagine again that you are hiking along the path as described above.
At the maximum of your elevation, the steepest direction of the
hillside would be to your sides, perpendicular to your path. That is,
your path is perpendicular to the gradient of the function that
describes the elevation, and tangent to the level sets (or
contours) of the function. This is suggested in the figure above.
The path is a level set of the function G, and so the
gradient of G must also be perpendicular to the path. That is,
the gradients of f and G must be perpendicular,
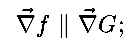
in the figure below, the arrow represents the common direction of the
gradients.
But, if two
vectors are parallel, their cross product must be zero, which in this
case would mean that the condition for an extreme subject to the
constraint is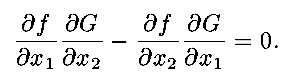
If we note that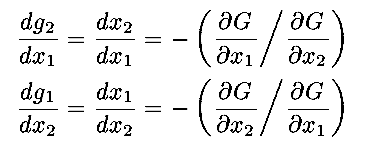
we see that
the above relations are recovered.
A generalization of the above method is shown in the next section, Lagrange Multipliers.
Examples:
For both of these examples, the function whose extremes are to be
found is the distance from a specified point. However, we recognize
that maximizing the square of a distance maximizes the distance, and
saves a good deal of work.
(1) Find the point on the line
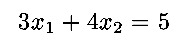
that is closest to the
origin. In this case,
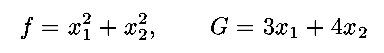
so that
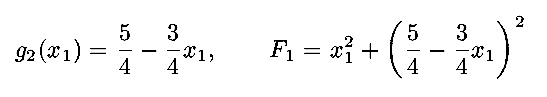
may be
found explicitly. Differentiating and setting equal to zero
gives
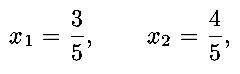
where the second
coordinate is found from the constraint G=5.
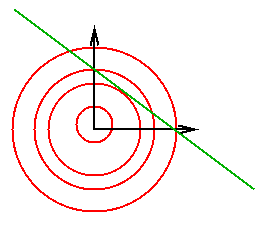
The situtation is illustrated below; it can be seen that at the
closest point, the line is tangent to a circle centered at the
origin. (In this rigged problem, the tangent circle is the unit circle.)
(2) Find the point on the parabola
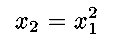
that is closest
to the point (0,a).
In this case,
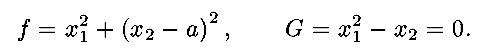
and
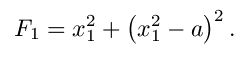
(Note that finding one variable as an explicit function of the other
is already done.) Differentiating and setting equal to zero gives
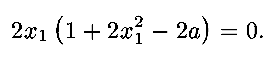
In solving this, you
must be careful: How many roots do you obtain, and why does the
number of roots depend on the value of a? Are the solutions
maxima or minima of the distance from the point? A figure (which you
can draw yourself) might help.
Vector Calculus Index |
World Web Math Main Page
watko@athena.mit.edu
Last modified February 10, 1999
 Constrained Min/Max
Constrained Min/Max Constrained Min/Max
Constrained Min/Max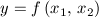 , then
, then