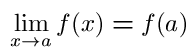Continuity
Continuity
Pre-requisites: Continuous
Functions., Limits.
Just like before, a scalar valued function of several variables is
continuous at a point if and only if
- it is
defined at that point and if the limit of the function is the point.
That is if f is the function in question and a is the point
- f(a) exists.
- f(x) must have a limit as x approaches a.
-
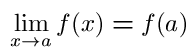
Definition: A curve is simply a continuous map from an interval in R to
R2 or R3. A curve
sigma(t): I -> R3 is graphed by plotting all
the points in its image, sigma(I) = { sigma(t): t in I }.
Here are some examples of curves:
- Lines. Here the interval I is taken to be all of R, and
the curve is l(t) = OP + t v. If you want a ray
instead of a line, make I into [0,infinity), and if you want a line
segment let I be a closed interval [a,b].
- A circle. I = [0,2 pi] and sigma(t) = ( cos t, sin t ).
A circle is a closed curve because sigma(0) = sigma(2 pi).
cos t and sin t are called the component functions of the curve.
A subarc of the circle, I = [a,b] with 0 < a < b < 2 pi would not be
closed because the ends of the subarc, sigma(a) and
sigma(b), would not be equal.
- A helix. sigma(t) = ( cos t, sin t, t ) and I = R.
- The graph of a continuous function f(t) can be made into a curve
by setting sigma(t) = ( t, f(t) ).
Vector Calculus Index |
World Web Math Main Page
watko@athena.mit.edu
last modified November 7, 1998
 Continuity
Continuity Continuity
Continuity