Scalar Valued Functions Scalar Valued FunctionsDefinition: A scalar field is a broad term for functions who take in points in a two or three dimensional space (R2 or R3) and outputs real numbers. The scalar field is a concept spawn from the natural and physical sciences since they often deal with a region of physical space with a function attached to it. For example, the function that gives the temperature of any point in the room you are sitting is a scalar field.You should note that a function doesn't need to expressed and defined as a mathematical formulat for it to be an explicit function. (Good luck figuring out the function for the temperature of every spot in your room!) Just the input-output correspondence. So particular scalara field may be specified by a mathematical expression, or it may be a function whose value at any point could be obtained by physical measurement.
Scalar fields can be combined to form new scalar fields by the usual algebraic operations. Let f and g be scalar fields defined on the same domain and k be a scalar, a real number.
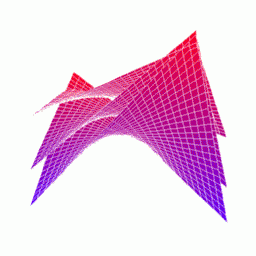
Level Curves are a tool for understanding and expressing the basic nature of two variable functions. Say we want to get a visual feel for the surface generated by a two variable function. One way to look at this surface is to make a topological map, or contour map, of the surface, like what mapmakers make when they want a map to be able to give information about elevation and the rugged lie of the land. Say we have a function z=f(x,y). We can generate a contour map of the surface by, for any value c that the function f assumes, sketching the function f(x,y)=c in the x-y plane. This curve is called a level curve. Notice that this curve also marks a path along which the value of f doesn't change.
The figure on the left of f=y sin x, is turned into a map of level curves on the right.
Level Surfaces
When dealing with three-variable functions, whose graphs are four-dimensional, level surfaces become a valuable tool for visualizing the behavior of a function. Like level curves, level surfaces are produced by setting a three variable function f(x,y,z) = c for various values of c. Level surfaces are more difficult to draw but provide an intuitive grasp of functions that don't fit in our brain. Notice again that a level surface represents no change in the function f.
