Fundamentals
Optical forces | Force fields | Lorentz force distribution in media | Modeling
Figure 1: Lorentz force density (arrows) within
a 2-D particle overlayed on total electric field
magnitude. (B. A. Kemp, T. M. Grzegorczyk,
and J. A. Kong, Comparison of methods for the
calculation of radiation pressure on dielectric
and magnetic particles, PIERS Cambridge, 2006).
Lorentz force distribution in media
Radiation pressure forces are often described in terms of scattering, gradient, and binding force components. The exact calculation of the forces on particles results from the change in electromagnetic momentum due to scattering, which is formalized by the divergence of the Maxwell stress tensor. A more fundamental view results from the direct application of the Lorentz force to the total fields in the presence of material. This force exists everywhere in the media as soon as the optical field is present. In this view, the scattering force is viewed as the force density following the gradient of the total field intensity, which results from the strong forward scattering [Fig. 1].
This force distribution in media is easily visualized for a plane-wave normally incident upon a lossless slab. The radiation pressure on the slab results from the distribution of Lorentz force density on bound currents. This force distribution tends to stretch and compress the regions in the slab, as well as account for the net radiation pressure [see Fig. 2, Fig. 3, and Fig. 4]. The radiation pressure due to arbitrary incidence reduces to a simple expression of momentum conservation,
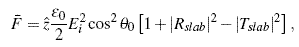
where θ0 is the incident angle and Rslab and Tslab are the slab reflection and transmission coefficients [Ref. 1]. This results in a cyclical function with respect to slab thickness [Fig. 5]. In addition to the volume force density, a surface force density on bound currents is necessary to model arbitrary incidence, and correctly predicts zero force at the Brewster angle of incidence [Fig. 6].
The Lorentz force density predicts, in accord with known experiments, the macroscopic behavior of particles a Gaussian beam [Fig. 7, Fig. 8] and in arbitrary incident optical landscapes [Fig. 9, Fig. 10]. A particle subject to a complex field pattern [Fig. 11] may also experience complex force patterns in addition to a net force [Fig. 12, Fig. 13]. This allows us to identify regions in the particles that are subject to high force concentration.
References
- Brandon A. Kemp, Tomasz M. Grzegorczyk, and Jin Au Kong, Ab initio study of the radiation pressure on dielectric and magnetic media, Optics Express, vol. 13, no. 23, pp. 9280-9291, 14 November, 2005.
- B.A. Kemp, T.M. Grzegorczyk, and J.A. Kong, Lorentz Force on Dielectric and Magnetic Particles, J. of Electromagn. Waves and Appl., vol. 20, no. 6, pp. 827-839, 2006.
