Image by Colin M. L. Burnett.
Every physicist knows the atom does not really look like this, but the archetype has a kind of insidious, mythical power that is hard to escape. One notes first the roundness of this "atom", a quality which the ancient Greeks would have admired. The p, d, and f states of real atoms, as imagined in the Twentieth Century quantum-mechanical paradigm, inherit the complicated forms of the Legendre polynomials, but when one thinks of an atom, one automatically thinks of spheres, not of spherical harmonics. It is interesting that, while the simple Bohr model (with its atom as flat as the ecliptic) is the only part of Old Quantum Mechanics still routinely taught to students today, it is Sommerfeld's modification, with ellipses pointing in all directions for approximate spherical symmetry, that seems to inform the popular stereotype.
Likewise, although the standard Copenhagen interpretation insists that electrons are not really particles and not really moving, intuition tells us that they are planets in a Rutherfordian solar system, hurtling around the nucleus. However much one insist that only a probability distribution can be measured, and that "momentum" is just an imaginary gradient-operator in Hilbert space, the notion of an orbital path along which the electron moves with some velocity remains unexorcised. "The unusual properties of gold are due to the relativistic speed at which the electron goes ripping by the nucleus ..."
I still recall my first encounter with the Bohm theory, in the form of an extremely abbreviated synopsis presenting little more than the main idea of rewriting Schrödinger's equation in terms of action and quantum potential. I immediately sat down and tried to solve the hydrogen atom, but stopped in amazement when I saw that an electron in the ground state must be at rest. Surely I had made some mistake! Unable to see any, I walked to the library (as one did in those pre-Wikipedian days) to find a fuller account of Bohmian mechanics. Having confirmed that my result was indeed standard, I temporarily lost interest in the theory: an electron that stands still seemed too ludicrous to consider.
Given the strength of these prejudices, it is surprising to realise that they are not, in fact, very old. The sphericity of atoms was (surprisingly) not considered self-evident by the Greeks or their successors; the curious shapes advocated by Dalton at the beginning of modern chemistry are of course well knowm. When chemical atoms ceased to be "atomic" and were resolved into constituent parts, the motion of these parts was not taken for granted: raisins do not hurtle about in a plum pudding!
Physicists traditionally study basic astronomy and celestial mechanics in their student days; probably for this reason, the solar-system atom and its modification by Bohr rapidly gained acceptance in the physics world. Chemists, on the other hand, are more at home with crystals, and the concept of the atom as a kind of "unit cell" persisted among chemists well into the 1920s.
The most famous advocate of this approach was G. N. Lewis, whose "dot diagrams", still used today, were originally meant to illustrate the properties of a cubical atom with valence electrons sitting motionless at its vertices. A cube has eight corners -- hence, according to Lewis, the Octet Rule.
Among the most brilliant advocates of this general approach --- he did not see eye-to-eye with Lewis on every detail --- was the great Irving Langmuir. Here we see him on the cusp of the quantum age, defending the chemical view against the Rutherford-Bohr onslaught.
The Structure of the Static Atom by Irving Langmuir [Science 53, 290 (1921)] Langmuir's words are in bold.

In attempting recently to derive the conditions which determine the stability of chemical molecules I was impressed by the importance of the part played by Coulomb's law of inverse square forces between charged particles. In fact, by considering a static arrangement of electrons according to the models which I proposed two years ago, and calculating the total potential energy by Coulomb's law, I have found it possible not only to determine the relative stability of various substances but to calculate with reasonable accuracy the heats of formation of compounds even of widely varying types.
In all such calculations, however, it is necessary to assume that the electrons are kept from falling into the nucleus by some undetermined force, for Coulomb's law alone can not account for this. According to Bohr's theory of atomic structure, the requisite repulsive force is nothing more than centrifugal force due to rotation of the electrons about the nucleus. This theory has been so remarkably successful in accounting for the spectra of hydrogen and helium that the fundamental assumption of movement about the nucleus has seemed justified, notwithstanding the fact that this violates all our classical laws regarding the radiation of energy from accelerated electrons.
From the chemical point of view it is a matter of comparative indifference what the cause of the repulsive force is, so long as it exists. I therefore endeavored to find what law of repulsive force between electrons and positive nuclei would produce an effect equivalent to the centrifugal force of Bohr's theory.
According to Bohr the average kinetic energy in any atom or molecule is half as great as the average potential energy, but opposite in sign. I therefore now assume that this energy, which Bohr called kinetic, is another form of potential energy dependent upon certain quantum changes in the electron. From this potential energy it is then easy to determine the law of repulsive force.
The result of this analysis is that we may regard the force between any nucleus of charge Ze and an electron of charge e as consisting of two parts which act independently. The first is the Coulomb attractive force Fe given by
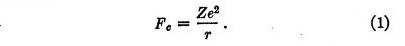
The second force, which we may call the quantum force, is a repulsive force Fq given by
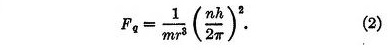
In these equations r is the distance between the electron and the nucleus, m is the mass of the electron, h is Planck's quantum, and n is an integer denoting the quantum state of the electron. This repulsive force, varying inversely as the cube of the distance, is remarkable in that it is independent of the charge on the nucleus.
It is to be noted especially that an electron which has not undergone any quantum change and for which therefore n = 0, follows Coulomb's law accurately. Thus presumably β-rays in passing through an atom will be acted on only by the usual law.
It can be readily shown that under the influence of these two forces an electron will be in stable equilibrium when it is at a distance from the nucleus equal to
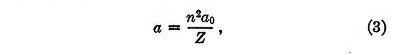
where a0 is given by
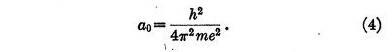
This result is identical with that for the radius of the orbit in Bohr's theory, but of course the law of force was chosen to give just this result.
If W is the total energy of the system with its sign reversed we obtain
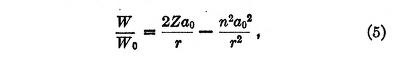
where
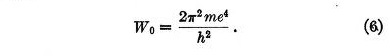
Equation (5) has no equivalent in Bohr's theory for it applies to the transitions between stationary states. The first term in the second member represents the Coulomb potential while the second corresponds to the quantum potential.
When an electron has settled down into its position of equilibrium, the value of W becomes
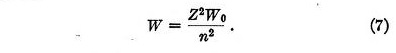
This also is identical with the result obtained by Bohr for the total energy in any stationary state. It follows from this that the Rydberg constant, the Balmer series and all other series calculated by Bohr can be obtained by this method without assuming electrons moving about the nucleus.
If the electron is disturbed from its position of equilibrium it oscillates about this position. From equation 5 the frequency of this oscillation is found to be
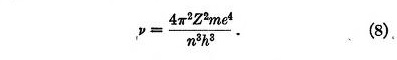
This is identical with the frequency of revolution of the electron in Bohr atom. From this we may draw a definite physical picture of the mechanism of the transition between two states, at least when Z is large. Bohr has shown that under these conditions the frequency radiated when an electron passes from one circular orbit to the next inner one is the same as the frequency of revolution. According to the present theory, if the quantum number of an electron in a stable position decreases by one unit, the electron is no longer stable but falls towards its new position of equilibrium, and oscillates about this position. It then radiates its energy of oscillation according to the usual laws of electro-dynamics.
One of the greatest successes of the Bohr theory is that it accounts for certain slight differences between hydrogen and helium lines by the nuclear mass correction. This correction is taken care of in the present theory with the same accuracy if we assume a slight modification to our law of quantum repulsion, viz. replace equation (2) by
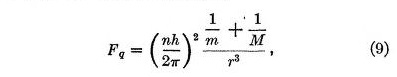
where M is the mass of the nucleus. This seems to indicate that the quantum force is due to an interaction between the electron and the nucleus in which both masses play a similar rôle. For example, it may be imagined that both are set into rotation in opposite directions about the axis connecting them.
Sommerfeld has accounted for the fine-line structure of spectral lines by considering a relativity correction due to the rapid motion of the electron. This would seem to be excellent proof that the electrons do move. However, it is possible that the motion resides within the electron and nucleus. It is probably significant that the relativity correction can be taken into account in the present theory if we substitute in equation 2 in place of n2 the expression
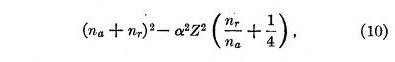
where α is a constant calculated by Sommerfeld. A consideration of this equation may lead to more definite conceptions of the structure of the electron and nucleus. The quantities na and nr refer to what Sommerfeld calls angular and radial quanta. It is not yet clear just what interpretation is to be placed upon these in the present theory but they are evidently only of secondary importance in determining the forces between the electrons and the nucleus.
When we consider other atoms such as helium it seems as if the new theory may lead us much further than the usual theory, for the determination of equilibrium positions under static forces is extremely simple compared to the corresponding dynamical problem. Furthermore we are not troubled by mysterious quantum conditions which are theoretically applicable only to periodic orbits while the calculated orbits in atoms are not periodic.
At present I am studying the spectra of helium and lithium from this viewpoint. The following tentative conclusions may be stated.
The quantum force between quantized electrons is not as simple as between electrons and nuclei. The quantum force between electrons on opposite sides of a nucleus is one of repulsion whose magnitude is approximately given by equation (2) if the quanta are all of the "angular" type, but is considerably less when the quanta are of the "radial " type. But if the electrons are on the same side of the nucleus, the quantum force between electrons is one of attraction, also given approximately by equation (2). Thus if one of the electrons in the helium is uniquantic, and the other one is diquantic, the latter can take equilibrium positions either on the opposite side of the nucleus from the uniquantic electron or on the same side. This perhaps explains the fact that helium (as well as other elements with two outer electrons such as calcium, etc.) has two separate complete sets of spectra (helium and parhelium). It is also in accord with the remarkable facts in regard to the helium spectrum which were recently pointed out by Franck and Reiche.
These properties of the electron are in full accord with those which are needed to account for chemical relationships. The new theory fulfills the predictions of G. N. Lewis who in 1916 [Jour. Amer. Chem. Soc., 38, 773] wrote in reference to Bohr's theory :
"Now this is not only inconsistent with the accepted laws of electromagnetics but, I may add, is logically objectionable, for that state of motion which produces no physical effect whatsoever may better be called a state of rest."
It is also in accord with the conclusion which I gave in a paper entitled "The properties of the electron as derived from the chemical properties of the elements," [Phys. Rev., 8, 300 (1919)] viz.:
"How can these results be reconciled with Bohr's theory and with our usual conception of the electron? It is too early to answer. Bohr's stationary states and the cellular structure postulated above have many points of similarity. It seems that the electron must be regarded as a complex structure which undergoes a series of discontinuous changes while it is being bound by the nucleus or kernel of an atom. There seems to be strong evidence that an electron can exert magnetic attractions on other electrons in the atom even when not revolving about the nucleus of the atom."
Irving Langmuir
Research Laboratory,
General Electric Co.,
Schenectady, N. Y.,
March 8, 1921
Those were confusing times, and although Langmuir's discussion of electron-electron interactions seems a bit like special pleading, one could find instances of similar language used by the school of Bohr.
A modern reader (or at least this modern reader) cannot read this essay without being struck by its (admittedly dim) prefiguration of the Bohmian attitude -- right down to the name "quantum potential"! The Lewisite position, in its essence, was that quantum phenomena are the result of a new force acting on microscopic objects; this is as close to Bohm's interpretation of quantum mechanics as the old Bohr atom is to Copenhagen. One could easily imagine an alternate history in which Lewisites developed wave mechanics first, and (what we would call) the Bohmian approach became the standard one throughout the 1900s.

Lewis's notes, 1902. [California State University Los Angeles]