DIFFERENCE ENGINE NO. I.
"Oh no ! we never mention it,
Its name is never heard."
Difference Engine No. 1 --- First Idea at Cambridge, 1812
Calculating Machines comprise various pieces of mechanism for assisting the human mind in executing the operations of arithmetic. Some few of these perform the whole operation without any mental attention when once the given numbers have been put into the machine.
Others require a moderate portion of mental attention: these latter are generally of much simpler construction than the former, (and it may also be added, are less useful).
The simplest way of deciding to which of these two classes any calculating machine belongs is to ask its maker whether, when the numbers on which it is to operate are placed in the instrument, it is capable of arriving at its result by the mere motion of a spring, a descending weight, or any other constant force. If the answer be in the affirmative, the machine is really automatic ; if otherwise, it is not self-acting.
[In the 1800s the word "automatic" was slowly acquiring its modern sense of "mechanical". In Greek, the word means "acting on its own" with the connotations "spontaneously" or even "at random".]
Of the various machines I have had occasion to examine, many of those for Addition and Subtraction have been found to be automatic. Of machines for Multiplication and Division, which have fully come under my examination, I cannot at present recall one to my memory as absolutely fulfilling this condition.
The earliest idea that I can trace in my own mind of calculating arithmetical Tables by machinery arose in this manner : ---
One evening I was sitting in the rooms of the Analytical Society, at Cambridge, my head leaning forward on the Table in a kind of dreamy mood, with a Table of logarithms lying open before me. Another member, coming into the room, and seeing me half asleep, called out, "Well, Babbage, what are you dreaming about ?" to which I replied, "I am thinking that all these Tables (pointing to the logarithms) might be calculated by machinery."
I am indebted to my friend, the Rev. Dr. Robinson, the Master of the Temple, for this anecdote. The event must have happened either in 1812 or 1813.
About 1819 I was occupied with devising means for accurately dividing astronomical instruments, and had arrived at a plan which I thought was likely to succeed perfectly. I had also at that time been speculating about making machinery to compute arithmetical Tables.
One morning I called upon the late Dr. Wollaston, to consult him about my plan for dividing instruments. On talking over the matter, it turned out that my system was exactly that which had been described by the Duke de Chaulnes, in the Memoirs of the French Academy of Sciences, about fifty or sixty years before. I then mentioned my other idea of computing Tables by machinery, which Dr. Wollaston thought a more promising subject.
I considered that a machine to execute the mere isolated operations of arithmetic, would be comparatively of little value, unless it were very easily set to do its work, and unless it executed not only accurately, but with great rapidity, whatever it was required to do.
On the other hand, the method of differences supplied a general principle by which all Tables might be computed through limited intervals, by one uniform process. Again, the method of differences required the use of mechanism for Addition only. In order, however, to insure accuracy in the printed Tables, it was necessary that the machine which computed Tables should also set them up in type, or else supply a mould in which stereotype plates of those Tables could be cast.
I now began to sketch out arrangements for accomplishing the several partial processes which were required. The arithmetical part must consist of two distinct processes : the power of adding one digit to another, and also of carrying the tens to the next digit, if it should be necessary.
The first idea was, naturally, to add each digit successively. This, however, would occupy much time if the numbers added together consisted of many places of figures.
The next step was to add all the digits of the two numbers each to each at the same instant, but reserving a certain mechanical memorandum, wherever a carriage became due [i.e. whenever a digit had to be carried to the next column]. These carriages were then to be executed successively.
Having made various drawings, I now began to make models of some portions of the machine, to see how they would act. Each number was to be expressed upon wheels placed upon an axis ; there being one wheel for each figure in the number operated upon.

Addition and carry mechanism of Difference Engine No. 1, assembled from the original parts by Babbage's son in the 1870s. Now in the Whipple Museum, Cambridge. Photo © Andrew Dunn, 2004
Having arrived at a certain point in my progress, it became necessary to have teeth of a peculiar form cut upon these wheels. As my own lathe was not fit for this job, I took the wheels to a wheel-cutter at Lambeth, to whom I carefully conveyed my instructions, leaving with him a drawing as his guide.
These wheels arrived late one night, and the next morning I began putting them in action with my other mechanism, when, to my utter astonishment, I found they were quite unfit for their task. I examined the shape of their teeth, compared them with those in the drawings, and found they agreed perfectly ; yet they could not perform their intended work.
I had been so certain of the truth of my previous reasoning, that I now began to be somewhat uneasy. I reflected that, if the reasoning about which I had been so certain should prove to have been really fallacious, I could then no longer trust the power of my own reason. I therefore went over with my wheels to the artist who had formed the teeth, in order that I might arrive at some explanation of this extraordinary contradiction.
On conferring with him, it turned out that, when he had understood fully the peculiar form of the teeth of wheels, he discovered that his wheel-cutting engine had not got amongst its divisions that precise number which I had required. He therefore had asked me whether another number, which his machine possessed, would not equally answer my object. I had inadvertently replied in the affirmative. He then made arrangements for the precise number of teeth I required ; and the new wheels performed their expected duty perfectly.
The next step was to devise means for printing the tables to be computed by this machine. My first plan was to make it put together moveable type. I proposed to make metal boxes, each containing 3,000 types of one of the ten digits. These types were to be made to pass out one by one from the bottom of their boxes, when required by the computing part of the machine.
But here a new difficulty arose. The attendant who put the types into the boxes might, by mistake, put a wrong type in one or more of them. This cause of error I removed in the following manner : ---
There are usually certain notches in the side of the type. I caused these notches to be so placed that all the types of any given digit possessed the same characteristic notches, which no other type had. Thus, when the boxes were filled, by passing a small wire down these peculiar notches, it would be impeded in its passage, if there were included in the row a single wrong figure. Also, if any digit were accidentally turned upside down, it would be indicated by the stoppage of the testing wire.
One notch was reserved as common to every species of type. The object of this was that, before the types which the Difference Engine had used for its computation were removed from the iron platform on which they were placed, a steel wire should be passed through this common notch, and remain there. The tables, composed of moveable types, thus interlocked, could never have any of their figures drawn out by adhesion to the hiking-roller, and then by possibility be restored in an inverted order. (A small block of such figures tied together by a bit of string, remained unbroken for several years, although it was rather roughly used as a plaything by my children.) One such box was finished, and delivered its type satisfactorily.
Another plan for printing the tables, was to place the ordinary printing type round the edges of wheels. Then, as each successive number was produced by the arithmetical part, the type-wheels would move down upon a plate of soft composition, upon which the tabular number would be impressed. This mould was formed of a mixture of plaster-of-Paris with other materials, so as to become hard in the course of a few hours.
The first difficulty arose from the impression of one tabular number on the mould being distorted by the succeeding one.
I was not then aware that a very slight depth of impression from the type would be quite sufficient. I surmounted the difficulty by previously passing a roller, having longitudinal wedge-shaped projections, over the plastic material. This formed a series of small depressions in the matrix between each line. Thus the expansion arising from the impression of one line partially filled up the small depression or ditch which occurred between each successive line.
The various minute difficulties of this kind were successively overcome ; but subsequent experience has proved that the depth necessary for stereotype moulds is very small, and that even thick paper, prepared in a peculiar manner, is quite sufficient for the purpose.
Another series of experiments were, however, made for the purpose of punching the computed numbers upon copper plate. A special machine was contrived and constructed, which might be called a co-ordinate machine, because it moved the copper plate and steel punches in the direction of three rectangular co-ordinates. This machine was afterwards found very useful for many other purposes. It was, in fact, a general shaping machine, upon which many parts of the Difference Engine were formed.
Several specimens of surface and copper-plate printing, as well as of the copper plates, produced by these means, were exhibited at the Exhibition of 1862.
I have proposed and drawn various machines for the purpose of calculating a series of numbers forming Tables by means of a certain system called "The Method of Differences," which it is the object of this sketch to explain.

Difference Engine No. 1: working replica at the Science Museum in London.
The first Difference Engine with which I am acquainted comprised a few figures, and was made by myself, between 1820 and June 1822. It consisted of from six to eight figures. A much larger and more perfect engine was subsequently commenced in 1823 for the Government.
It was proposed that this latter Difference Engine should have six orders of differences, each consisting of about twenty places of figures, and also that it should print the Tables it computed.
The small portion of it which was placed in the International Exhibition of 1862 was put together nearly thirty years ago. It was accompanied by various parts intended to enable it to print the results it calculated, either as a single copy on paper --- or by putting together moveable types --- or by stereotype plates taken from moulds punched by the machine --- or from copper plates impressed by it. The parts necessary for the execution of each of these processes were made, but these were not at that time attached to the calculating part of the machine.
A considerable number of the parts by which the printing was to be accomplished, as also several specimens of portions of tables punched on copper, and of stereotype moulds, were exhibited in a glass case adjacent to the Engine.
In 1834 Dr. Lardner published, in the Edinburgh Review, (No. CXX, July, 1834) a very elaborate description of this portion of the machine, in which he explained clearly the method of Differences.
[Lardner not only wrote an excellent sixty-four page article on the Difference Engine, but also made a lecture tour around England promoting the device, asserting that Babbage's computer would replace error-riddled published mathematical tables with mechanical precision. His excessively polemical tone on this point offended the professional calculators responsible for the tables, and made them Babbage's sworn enemies.
One of his generation's leading "public intellectuals", Rev. Dionysius Lardner was on the founding faculty of the University of London, and the most widely-read English-language "popular science" writer in the first half of the Nineteenth Century; in both capacities, his importance for the dissemination of scientific knowledge in the early Victorian period would be hard to overstate. Nevertheless, he was controversial; many people saw him as an opinionated, vain, publicity-hungry quack. He appears in one of Thackeray's sketches (actually a sort of early comic strip) as Dionysius Diddler of Brentford, "by trade a philosopher, --- an excellent profession in Brentford, where people are more ignorant and more easily humbugged than any people on earth." Moreover, he was Irish, and the (numerous) satirical depictions of him by his contemporaries are full of anti-Celtic racial prejudice; Thackeray's Diddler longs for his alma mater, the University of Ballybunion in the hedge, saying "I'm femous all the world over, but what's the use of riputetion? I'd give all me celebrity for a bowl of butter-milk and potaties." He was also notorious for his personal life: in spite of being an ordained Anglican clergyman, he was divorced, had a son by the married sister of the astronomer-poet George Darley, and eventually ran off to America with an Army officer's wife. All in all, the fact that Lardner was Babbage's most outspoken champion could not have been an unmixed blessing.]
It is very singular that two persons, one resident in London, the other in Sweden, should both have been struck, on reading this review, with the simplicity of the mathematical principle of differences as applied to the calculation of Tables, and should have been so fascinated with it as to have undertaken to construct a machine of the kind.
Mr. [Alfred] Deacon, of Beaufort House, Strand, whose mechanical skill is well known, made, for his own satisfaction, a small model of the calculating part of such a machine, which was shown only to a few friends, and of the existence of which I was not aware until after the Swedish machine was brought to London.
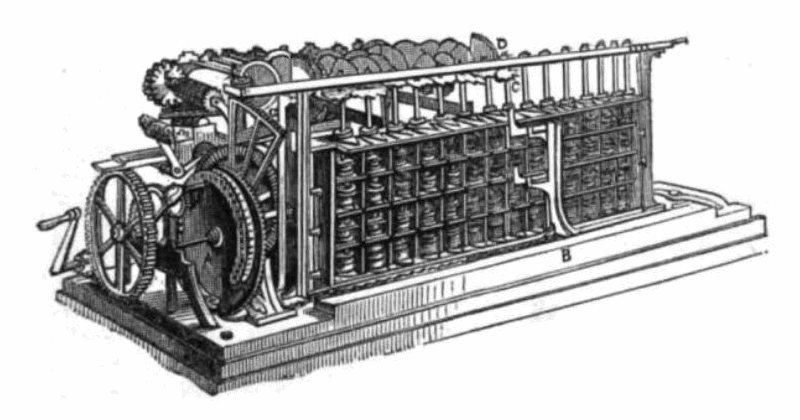
Scheutz's difference-engine (from The Elements of Natural Philosophy by C. Brooke and G. Bird [London: Churchill (1867)])
Mr. [Pehr-Georg] Scheutz, an eminent printer at Stockholm, had far greater difficulties to encounter. The construction of mechanism, as well as the mathematical part of the question, was entirely new to him. He, however, undertook to make a machine having four differences, and fourteen places of figures, and capable of printing its own Tables.
After many years' indefatigable labour, and an almost ruinous expense, aided by grants from his Government, by the constant assistance of his son, and by the support of many enlightened members of the Swedish Academy, he completed his Difference Engine. It was brought to London, and some time afterwards exhibited at the great Exhibition at Paris. It was then purchased for the Dudley Observatory at Albany [N. Y.] by an enlightened and public-spirited merchant of that city, John F. Rathbone, Esq. [The full story of this incident may be read online in a genealogical publication, Rathbun-Rathbone-Rathburn Family History, October 1988.]
An exact copy of this machine was made by Messrs. Donkin and Co., for the English Government, and is now in use in the Registrar-General's Department at Somerset House. It is very much to be regretted that this specimen of English workmanship was not exhibited in the International Exhibition.
