
The Kelvin Memorial at the University of Glasgow. Photo by Yuriy "Yuriybrisk" Lapitskiy, 2005.

Sir William Thomson, later Lord Kelvin, was among the Nineteenth Century's most brilliant, most intellectually ambitious, and in his lifetime most honoured physicists. Today, though certainly remembered and admired, he comes across as secondary figure, eclipsed by Faraday, Maxwell, and the German thermodynamicists. This is perhaps because no great foundational paradigm is associated primarily with his name. It might have been otherwise: throughout his later career, Kelvin developed and tirelessly promoted a unified theory of matter, electricity, and light grounded in classical fluid-mechanics, one of his personal specialities. Kelvin's æther model was taken seriously, but it failed to gain universal acceptance; its main legacy is knot theory, a branch of mathematics that Kelvin invented for his project of describing atoms as knotted vortex-lines in the æther. The very use of the word "æther" was of course enough to remove Kelvin's cosmology from any serious consideration for most of the Twentieth Century; only in the 1990s was it widely recognised as a precursor (or indeed as the forgotten origin) of string theory.
In 2015 string theory is itself in some degree of trouble, so Kelvin's ideas might be considered less relevant than ever. Curiously, this is not the case. The astonishing experiments with bouncing drops of liquid conducted since 2005 by Yves Couder and others have drawn attention to the use of classical fluids as quantum analogues, and have led some bold thinkers to re-examine the "double solution" version of de Broglie's pilot-wave interpretation of quantum mechanics. In such a context, Kelvin's vortex "atoms" may swirl to life once again.
The characteristically lucid and fairly non-technical address reproduced below is not only an excellent introduction to Kelvin's thought (at one stage of development) but also helps the modern reader understand in a more general way how the uniquely British concept of the æther as a literal machine, incorporating gears and fly-wheels, was gradually reconciled with the more familiar and "naturalistic" view of it as a space-filling jelly. Had this reconciliation never occurred, the history of relativity in the English-speaking world might have been very different indeed.
STEPS TOWARDS A KINETIC THEORY
OF MATTER.
Address to the mathematical and physical section of the
British association at Montreal, Aug. 28, 1884, by Professor Sir
William Thomson, M.A., LL.D., D.C.L., F.R.S., L. & E.,
F.R.A.S., president of the section.
[
Science 4, 204 (1884)].
Thomson's words are in bold
The now well-known kinetic theory of gases is a step so important, in the way of explaining seemingly static properties of matter by motion, that it is scarcely possible to help anticipating, in idea, the arrival at a complete theory of matter, in which all its properties will be seen to be merely attributes of motion.
Rich as it is in practical results, the kinetic theory of gases, as hitherto developed, stops absolutely short at the atom or molecule, and gives not even a suggestion towards explaining the properties in virtue of which the atoms or molecules mutually influence one another.
Every one who has hitherto written or done anything very explicit in the kinetic theory of gases has taken the mutual action of molecules in collision as repulsive. May it not, after all, be attractive ?
Imagine a great multitude of particles enclosed by a boundary which may be pushed inwards in any part, all round, at pleasure. Now station an engineer corps of Maxwell's army of sorting demons all round the enclosure, with orders to push in the boundary diligently everywhere when none of the besieged troops are near, and to do nothing when any of them are seen approaching, and until after they have turned again inwards. The result will be, that, with exactly the same sum of kinetic and potential energies of the same enclosed multitude of particles, the throng has been caused to be denser.
Now, Joule's and Thomson's old experiments on the efflux of air prove, that if the crowd be common air, or oxygen, or nitrogen, or carbonic acid, the temperature is a little higher in the denser than in the rarer condition when the energies are the same. By the hypothesis, equality of temperature between two different gases, or two portions of the same gas at different densities, means equality of kinetic energies in the same number of molecules of the two. From the observations proving the temperature to be higher, it therefore follows that the potential energy is smaller in the condensed crowd. This (always, however, under protest as to the temperature hypothesis) proves some degree of attraction among the molecules, but it does not prove ultimate attraction between two molecules in collision, or at distances much less than the average mutual distance of nearest neighbors in the multitude.
We must look distinctly on each molecule as being either a little elastic solid, or a configuration of motion in a continuous, all-pervading liquid. How we can ever permanently rest anywhere short of this last view is not evident ; but it would be a very pleasant temporary resting-place on the way to it, if we could, as it were, make a mechanical model of a gas out of little pieces of round, perfectly elastic, solid matter, flying about through the space occupied by the gas, and colliding with one another, and against the sides of the containing vessel.
But alas for a mechanical model consisting of the cloud of little elastic solids flying about amongst one another! Though each particle have absolutely perfect elasticity, the end must be pretty much the same as if it were but imperfectly elastic. The average effect of repeated and repeated mutual collisions must be to gradually convert all the translational energy into energy of shriller and shriller vibrations of the molecule.
Even if this fatal fault in the theory did not exist, and if we could be perfectly satisfied with the kinetic theory of gases founded on the collisions of elastic solid molecules, there would still be beyond it a grander theory, which need not be considered a chimerical object of scientific ambition, --- to explain the elasticity of solids.
If we could make out of matter devoid of elasticity a combined system of relatively moving parts, which, in virtue of motion, has the essential characteristics of an elastic body, this would be at least a finger-post, pointing a way which we may hope will lead to a kinetic theory of matter. Any ideal system of material particles, acting on one another mutually through mass-less connecting springs, may be perfectly imitated in a model consisting of rigid links jointed together, and having rapidly rotating fly-wheels pivoted on some or on all of the links.
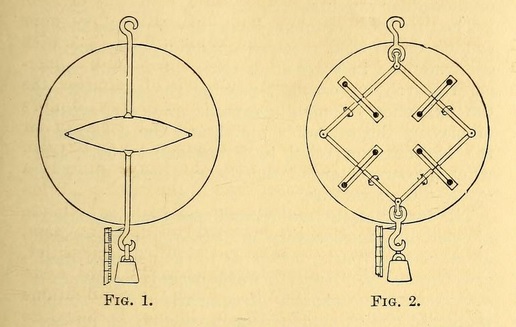
The drawings (figs. 1 and 2) illustrate two such material systems. The directions of rotation of the fly-wheels in the gyrostatic system (fig. 2) are indicated by directional ellipses, which show in perspective the direction of rotation of the fly-wheel of each gyrostat. The gyrostatic system (fig. 2) might have been constituted of two gyrostatic members, but four are shown for symmetry. The enclosing circle represents in each case, in section, an enclosing spherical shell to prevent the interior from being seen. In the inside of one there are fly-wheels ; in the inside of the other, a massless spring.
The projecting hooked rods seem as if they are connected by a spring in each case. If we hang any one of the systems up by the hook on one of its projecting rods, and hang a weight to the hook of the other projecting rod, the weight, when first put on, will oscillate up and down, and will go on doing so forever, if the system be absolutely unfrictional. If we check the vibration by hand, the weight will hang down at rest, the pin drawn out to a certain degree ; and the distance drawn out will be simply proportional to the weight hung on, as in an ordinary spring-balance.
Here, then, out of matter possessing rigidity, but absolutely devoid of elasticity, we have made a perfect model of a spring in the form of a spring-balance. Connect millions of millions of particles by pairs of rods such as these of this spring-balance, and we have a group of particles constituting an elastic solid.
The gyrostatic model spring-balance is arranged to have zero moment of momentum [angular momentum] as a whole, and therefore to contribute nothing to the Faraday rotation. With this arrangement, the model illustrates the luminiferous ether in a field unaffected by magnetic force.
But now let there be a different rotational velocity imparted to the jointed square, round the axis of the two projecting hooked rods, such as to give a resultant moment of momentum round any given line through the centre of inertia of the system, and let pairs of the hooked rods in the model thus altered, which is no longer a model of a mere spring-balance, be applied as connections between millions of pairs of particles, as before, with the lines of resultant moment of momentum all similarly directed: we now have a model elastic solid which will have the property that the direction of vibration in waves of rectilinear vibrations propagated through it shall turn round the line of propagation of the waves; just as Faraday's observation proves to be done by the line of vibration of light in a dense medium between the poles of a powerful magnet. The case of wave-front perpendicular to the lines of resultant moment of momentum (that is to say, the direction of propagation being parallel to these lines) corresponds, in our mechanical model, to the case of light travelling in the direction of the lines of force in a magnetic field.
But now, with the view of ultimately discarding the postulate of rigidity from all our materials, let us suppose some to be absolutely destitute of rigidity, and to possess merely inertia and incompressibility, and mutual impenetrability with reference to the still remaining rigid matter. With these postulates, we can produce a perfect model of mutual action at a distance between solid particles, fulfilling the condition, so keenly desired by Newton and Faraday, of being explained by continuous action through an intervening medium.
Imagine a solid bored through with a hole, and placed in our ideal perfect liquid. For a moment let the hole be stopped by a diaphragm, and let an impulsive pressure be applied for an instant uniformly over the whole membrane, and then instantly let the membrane be dissolved into liquid. This action originates a motion of the liquid relatively to the solid, of a kind to which has been given the name of irrotational circulation, which remains absolutely constant, however the solid be moved through the liquid.
Thus at any time the actual motion of the liquid, at any point in the neighborhood of the solid, will be the resultant of the motion it would have in virtue of the circulation alone were the solid at rest, and the motion it would have in virtue of the motion of the solid itself had there been no circulation established through the aperture.
It is interesting and important to remark, in passing, that the whole kinetic energy of the liquid is the sum of the kinetic energies which it would have in the two cases separately.
Now, imagine the whole liquid to be enclosed in an infinitely large, rigid containing-vessel ; and in the liquid, at an infinite distance from any part of the containing-vessel, let two perforated solids, with irrotational circulation through each, be placed at rest near one another. The resultant fluid motion due to the two circulations will give rise to fluid pressure on the two bodies, which, if unbalanced, will cause them to move.
It might be imagined that the action at a distance, thus provided for by fluid motion, could serve as a foundation for a theory of the equilibrium and the vibrations of elastic solids, and the transmission of waves like those of light through an extended quasi-elastic solid medium. But, unfortunately, the equilibrium is essentially unstable. If, however, we connect the perforated bodies, with circulation through them in the hydrokinetic system, by jointed rigid connecting-links, we may arrange for configurations of stable equilibrium.
Thus, without fly-wheels, but with fluid circulations through apertures, we may make a model spring-balance, or a model luminiferous ether, either without or with the rotational quality corresponding to that of the true luminiferous ether in the magnetic fluid ; in short, do all by the perforated solids, with circulations through them, that we saw we could do by means of linked gyrostats.
But something that we cannot do by linked gyrostats, we can do by the perforated bodies with fluid circulation: we can make a model gas. The mutual action at a distance, repulsive or attractive according to the mutual aspect of the two bodies when passing within collisional distance of one another, suffices to produce the change of direction of motion in collision, which essentially constitutes the foundation of the kinetic theory of gases.
There remains, however, as we have seen before, the difficulty of providing for the case of actual impacts between the solids.
Let us annul the solids, and leave the liquid performing irrotational circulation round vacancy, in the place of the solid cores which we have hitherto supposed ; or let us annul the rigidity of the solid cores of the rings, and give them molecular rotation according to Helmholtz's theory of vortex motion. As to whether, however, when the vortex theory of gases is thoroughly worked out, it will or will not be found to fail in a manner analogous to the failure already pointed out in connection with the kinetic theory of gases composed of little elastic solid molecules, one cannot at present speak with certainty.