The Net Advance of Physics: The Nature of Dark Matter, by Kim Griest -- Section 6D.

Accelerator Constraints

Extensive unsuccessful searches for the particles involved in

supersymmetric models have been performed at particle

accelerators throughout the world. This does not yet mean that

low-energy supersymmetry is unlikely to exist since only a small

portion of the mass range under 1 TeV has been explored. However,

substantial regions of prime neutralino dark matter parameter

space have been eliminated, and it is important to check this when

considering the detectability of any neutralino candidate. One does

not want to build a detector only capable of seeing particles ruled

out by current experiments. In the following, we demonstrate a

method of exploring supersymmetric parameter space taking into

account accelerator constraints in a rough way [22]. Note that the

same supersymmetric parameters which determine the relic

abundance cross sections determine all the particle production and

rare decay cross sections. Thus once these parameters are specified,

one can compare the model predictions with experimental results.

A partial list of relevant experimental results follows. Higgs

searches at LEP rule out the lightest scalar Higgs masses below

about 45 GeV, and pseudoscalar Higgs masses below about 39 GeV,

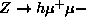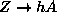using cross sections such as , and . LEP chargino

searches at the Z pole rule out 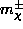below 45 GeV, and direct

neutralino searches constrain the branching ratio of Z into

neutralinos to be less than about 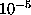. The squark and gluino

searches by CDF give complicated results, but one is probably safe if

one limits consideration to squarks with mass larger than 150 GeV.

Finally, the recent CLEO measurement of

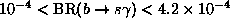
has important consequences for neutralinos. This is the decay of

bottom quarks into strange quarks plus a photon, and the

measurement is within the prediction of the standard model. The

impact on supersymmetry comes because this process can also occur

via exchange of supersymmetric particles and in many cases these

contributions can destroy the experimental agreement with the

standard model. So this branching ratio should also be computed for

every set of supersymmetric parameters, and models which do not

agree with the above constraint should be eliminated. We illustrate

the process by considering the grid of models in Figure 1 ([fig 1a],

[fig 1b], [captions]). Since the actual parameter space is five-

dimensional, this is just a two-dimensional projection of the

parameters. Figure 1(a) ([fig], [captions]) shows the entire grid

of models, while Figure 1(b) ([fig], [captions]) shows the models

which are left after eliminating those which violate an accelerator

constraint (or other consistency test).

Using just the allowed models we can now plot the neutralino mass

vs the relic abundance. The resulting plot (Figure 2 [fig], [captions])

is quite remarkable and can be taken as a hint that

supersymmetry may well have something to do with the dark

matter problem. Many models fall in the 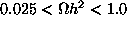range.

Recall that models with 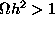imply a dark matter density

inconsistent with cosmological measurements. Thus dark matter

considerations can be used to help the particle physicists in their

search for supersymmetry; there is probably little use in considering

models which are inconsistent with cosmology (though as

experimentalists, it is probably wise that not too much weight is

given to such results). On the other hand, models with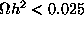

are perfectly viable from a particle physics point of view,

but predict too little relic abundance to make up all of the dark

matter. It is interesting to note, however, that even a relic

abundance of 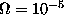would make neutralinos as

large a contributor as the microwave background. There was no

fine tuning invoked to produce the numerous models with relic

abundance in the proper range to be the dark matter, and it seems

that no matter what, if stable neutralinos exist, they must be an

important contributor to the mass inventory of the Universe.

BIBLIOGRAPHY