Bisection Methods:  10.001: Solution of Non-Linear  10.001: Solution of Non-Linear

Introduction

In this class, we will discuss algorithms for finding the roots of non-linear algebraic equations. The problem we are dealing with here can be stated mathematically as follows: Find values of x such that the non-linear equation, f(x)= 0 is satisfied. When we say f(x) is a non-linear function of x, it means that f(x) can not be written as a x + b , where a and b are constants. When we say that f(x) is an algebraic equation, it means that f(x) does not involve any differentials of the form dⁿy/dxⁿ. A simple example is that of the familiar quadratic equation where f(x) = ax² + bx + c = 0. Similarly, x-sin(x)=0 , x⁴ + 35x³ + 20 x² + x -3 = 0 etc. are all examples of non-linear equations. Evidently, the roots can not be obtained through analytical means except for a few simple cases. So our aim is to learn numerical methods which will evaluate the roots approximately.

There are many ways to locate an interval a < x < b where the curve defined by f(x)=0 intersects the x axis (the x coordinate of the point of intersection is a root of the equation f(x)=0). One way is to simply plot the function in a given interval. Another way is to find two points on the x axis, say x=a and x=b, such that the condition f(a)*f(b)< 0 is satisfied. i.e., the function changes sign as we move along the x axis from x=a to x=b (Let's assume that a < b. Moreover, we restrict our attention to real roots.). This implies, for continous functions, that the graph (curve) of the function y=f(x) intersects the x axis at least once between x=a and x=b.

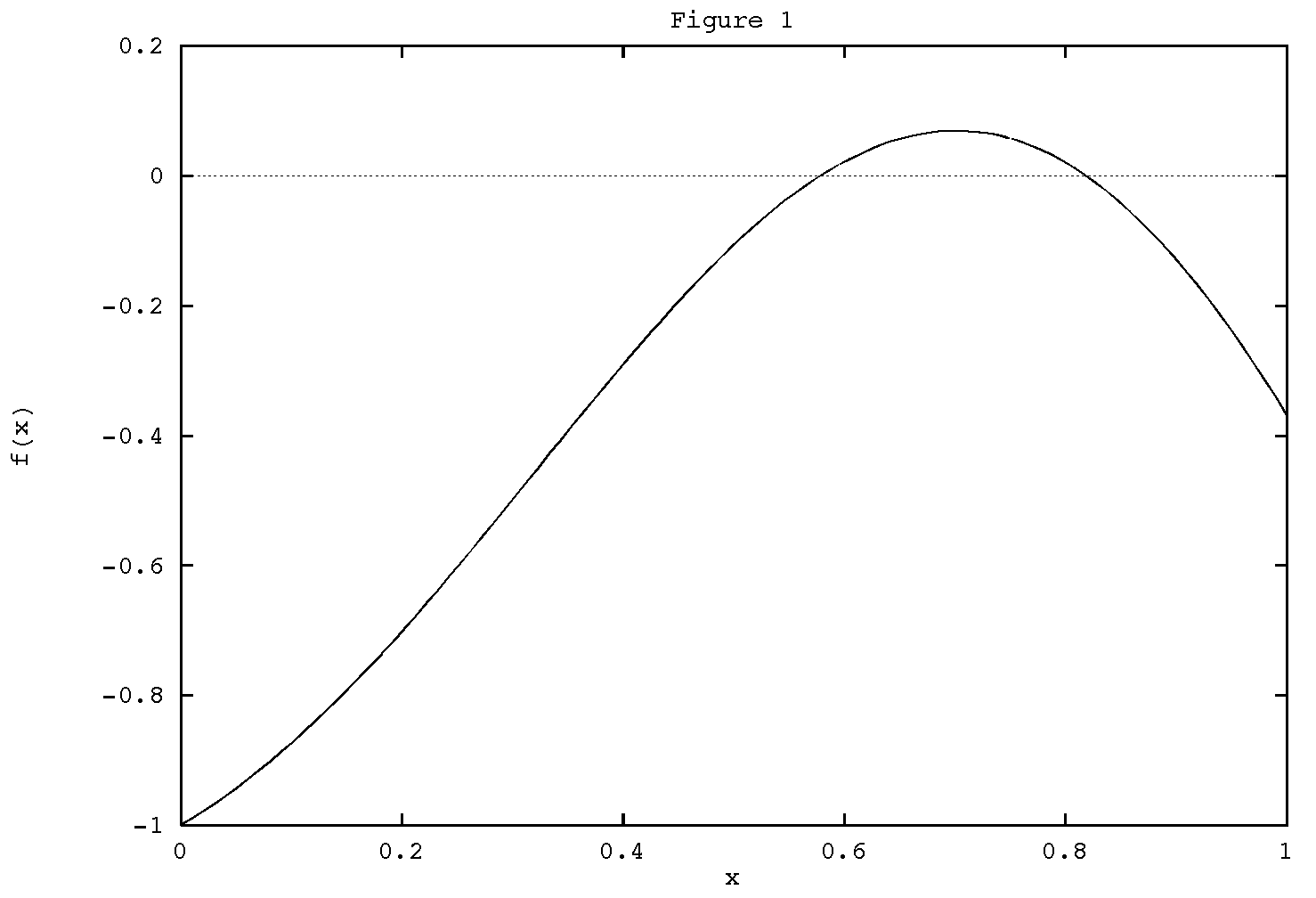
Example 1.: For instance, let f(x)=x*sin(pi x)-exp(-x). Since f(0)< 0 and f(2/3)>0 and since f(x) is continuous in this interval, there has to be a root between 0 and 2/3. Instead, we can simply plot the function using some mathematical software shown in Figure 1.

1998-10-01