- First Law of Thermodynamics
(VW, S & B: 2.6)
-
There exists for every system a property called energy. E = internal energy (arising from molecular motion - primarily a function of temperature) + kinetic energy + potential energy + chemical energy.
-
Defines a useful property called "energy".
-
The two new terms in the equation (compared to what you have seen in physics and dynamics, for example) are the internal energy and the chemical energy. For most situtations in this class, we will neglect the chemical energy.
-
Let’s focus on the internal energy, u. It is associated with the random or disorganized motion of the particles.
- The change in energy of a system is equal to the difference between the heat added to the system and the work done by the system. (This tells what the property energy is useful for.) (VW, S & B: Chapter 5)
-
The signs are important (and sometimes confusing!)
-
The equation can also be written on a per unit mass basis
- In many situations the potential energy and the kinetic energy of the system are constant.
-
Can also write the first law in differential form:
-
Or for quasi-static processes
-
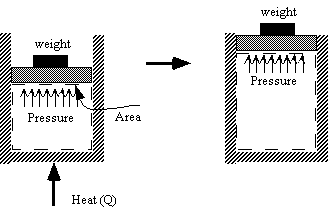
Example: Heat a gas, it expands against a weight. Force (pressure times area) is applied over a distance, work is done.
-
We will see later that the First Law can be written for a control volume with steady mass flow in and steady mass flow out (like a jet engine for example). We will call this the Steady-Flow Energy Equation. (VW, S & B: 5.8-5.12)
-
We will spend most of the course dealing with various applications of the first law - in one form or another.
u is a function of the state of the system. Thus u = u (p, T), or u = u (p, v), or u = u(v,T). Recall that for pure substances the entire state of the system is specified if any two properties are specified. We will discuss the equations that relate the internal energy to these other variables later in the class.
DE = Q - W (units are Joules)
E is the energy of the system
Q is the heat transferred to the system (positive) - if it is transferred
from the system Q is negative. (VW, S & B: 4.7-4.8)
W is the work done by the system (positive) - if work is done on
the system W is negative. (VW, S & B: 4.1-4.4)
De = q - w (units are J/kg)
Then De = Du, and
Du = q - w or DU = Q - W
Q and W are path dependent, U is not it depends only on the state of the system, not how the system got to that state.
dU = dQ - dW or du = dq - dw
Here the symbol "d" is used to denote that these are not exact differentials but are dependent on path.
dU = dQ - pdV or du = dq - pdv
- Corollaries of the First
Law
- Work done in any adiabatic (Q=0) process is path independent.
- For a cyclic process heat and work transfers are numerically equal


or
![]()
- Example applications of the
First Law to motivate the use of a property called "enthalpy"
(VW, S & B: 5.4-5.5)
- The combination u+pv shows up frequently so we give it a name: "enthalpy" h= u+pv (or H = U+pV). It is a function of the state of the system.
- Consider a quasi-static process of constant pressure expansion
- Consider adiabatic throttling of a gas (gas passes through a flow resistance). What is the relation between conditions before and after the resistance?
The utility and physical significance of enthalpy will be clearer when we discuss the steady flow energy equation in a few lectures. For now, you may wish to think of it as follows (Levenspiel, 1996). When you evaluate the energy of an object of volume V, you have to remember that the object had to push the surroundings out of the way to make room for itself. With pressure p on the object, the work required to make a place for itself is pV. This is so with any object or system, and this work may not be negligible. (Recall, the force of one atmosphere pressure on one square meter is equivalent to the force of a mass of about 10 tons.) Thus the total energy of a body is its internal energy plus the extra energy it is credited with by having a volume V at pressure p. We call this total energy the enthalpy, H.
Q = (U2 - U1) +W
= (U2 - U1) + p(V2 - V1) since p1 = p2 = p
so Q = (U2 + pV2) - (U1 + pV1) = H2 - H1

Q = 0 therefore DU = - DW
or U2 - U1 = -(p2V2 - p1V1)
so U2 + p2V2 = U1 + p1V1
H2 = H1
- First Law in terms of enthalpy
dU = dQ - dW (for any process, neglecting DKE and DPE)
dU = dQ - pdV (for any quasi-static process, no DKE or DPE)
H = U + pV therefore dH = dU + pdV + Vdp
so dH = dQ - dW + pdV + Vdp (any process)
or
dH = dQ + Vdp (for any quasi-static process)
- Specific Heats and Heat Capacity
(VW, S & B: 5.6)
-
Question
Throw an object from the top tier of the lecture hall to the front of the room. Estimate how much the temperature of the room has changed as a result. Start by listing what information you need to solve this problem.
- How much does a given amount of heat transfer change the temperature of a substance? It depends on the substance. In general
-
For a constant pressure process:
-
Expressions for u and h. Remember that if we specify any two properties of the system, then the state of the system is fully specified. In other words we can write u = u(T,v), u=u(p,v) or u=u(p,T) -- the same holds true for h. (VW, S & B: 5.7)
- Ideal gas assumption (VW, S & B: 5.7)
- First Law Expressions for an Ideal Gas
-
For an ideal gas undergoing a quasi-static process:
-
Relationships between thermodynamic properties cv, cp, and R
-
Equating the two first law expressions given above
-
The ratio of specific heats, g
- Questions:
-
On a p-v diagram for a closed-system sketch the thermodynamic paths that the system would follow if expanding from volume = v1 to volume = v2 by isothermal and quasi-static, adiabatic processes.
-
For which process is the most work done by the system?
-
For which process is there heat exchange? Is it added or removed?
-
Is the final state of the system the same after each process?
-
Derive expressions for the work done by the system for each process.
Q = CDT
where C is a constant that depends on the substance.
![]() or
or ![]()
and for a constant volume process:
![]() or
or ![]()
we use cp and cv to relate u and h to the temperature for an ideal gas.
Consider a constant volume process and write u = u(T,v). Then
![]()
where the last term is zero since there is no change in volume. Now if we write the First Law for a quasi-static process
du = dq - pdv
where again the last term is zero since there is no volume change. So
![]()
so
![]()
If we write h=h(T,p), and consider a constant pressure process, we can perform similar manipulations and show that
![]()
cp and cv are thermodynamic properties of a substance. The previous two relationships are valid at any point in any quasi-static process whether that process is constant volume, constant pressure, or neither.
If we have a thermally perfect gas (i.e. it obeys pv=RT), then it is called an ideal gas if u = u(T) only, and h= h(T) only. Then
![]()
and
![]()
so for an ideal gas

and

Over small temperature changes (DT Å 200K), it is often assumed that cp and cv are constant.
For an ideal gas, du=cvdT and dh=cpdT for any process (whether constant volume or constant pressure or not). This is an empirical fact for these special substances. If this is difficult to understand, put yourself in the position of an experimentalist who is attempting to measure cv for a substance. For such an experiment, you might add a known amount of heat to a rigid volume and measure the temperature change. Imagine repeating the experiment several times and getting the exact same answer, but one day finding out that during some of the repeats the volume was changing. This would be unusual and special and you might give this substance a special name. The special name we use for these substances is "ideal gas". (The same is true for cp. You might use a low friction piston-cylinder arragement with a fixed weight to maintain constant pressure while adding heat and measuring the temperature. Then one day you find that piston was getting stuck so the pressure was not constant afterall, but you still obtained the same temperature rise for the same amount of heat addition.)
dq = cvdT + pdv
or in terms of enthalpy
dq = cpdT - vdp
cpdT - vdp = cvdT + pdv
(cp - cv)dT = d(pv)
cp - cv = d(pv)/dT and pv = RT
so
cp - cv = R
g = cp/cv
dq = cvdT + pdv and dq = cpdT - vdp
so
cv dT = -pdv and cp dT = vdp
therefore
![]()
then
![]()
or
![]()
finally, we arrive at the very useful expression
pvg = constant
from which it can also be shown that

We will use the above equation to relate pressure and temperature to one another for quasi-static adiabatic processes (our idealization of what happens in compressors and turbines).