15.2 Fuel-Air Ratio
The reaction for aeroengine fuel at stoichiometric conditions is
On a molar basis, the ratio of fuel to air is
![$ [1/(12.5+47.0)] = 1/59.5 = 0.0167$](img1722.png) .
.
To find the ratio on a mass flow basis, which is the way in which
the aeroengine industry discusses it, we need to ``weight'' the
molar proportions by the molecular weight of the components. The
fuel molecular weight is
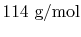 , the oxygen molecular
weight is
, the oxygen molecular
weight is
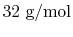 and the nitrogen molecular weight is
(approximately)
and the nitrogen molecular weight is
(approximately)
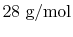 . The fuel/air ratio on a mass
flow basis is thus
. The fuel/air ratio on a mass
flow basis is thus
If we used the actual constituents of air we would get 0.0667, a
value about 0.5% different.
Muddy Points
Do we always assume 100% complete combustion? How good an
approximation is this?
(MP 15.3)
UnifiedTP
| 
