6.5 Irreversibility, Entropy Changes, and ``Lost Work''
Consider a system in contact with a heat reservoir during a
reversible process. If there is heat 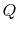 absorbed by the
reservoir at temperature
absorbed by the
reservoir at temperature  , the change in entropy of the reservoir
is
, the change in entropy of the reservoir
is
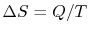 . In general, reversible processes are
accompanied by heat exchanges that occur at different temperatures.
To analyze these, we can visualize a sequence of heat reservoirs at
different temperatures so that during any infinitesimal portion of
the cycle there will not be any heat transferred over a finite
temperature difference.
. In general, reversible processes are
accompanied by heat exchanges that occur at different temperatures.
To analyze these, we can visualize a sequence of heat reservoirs at
different temperatures so that during any infinitesimal portion of
the cycle there will not be any heat transferred over a finite
temperature difference.
During any infinitesimal portion, heat
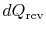 will be
transferred between the system and one of the reservoirs which is at
will be
transferred between the system and one of the reservoirs which is at
 . If
. If
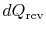 is absorbed by the system, the entropy
change of the system is
is absorbed by the system, the entropy
change of the system is
The entropy change of the reservoir is
The total entropy change of system plus surroundings is
This is also true if there is a quantity of heat rejected by the
system.
The conclusion is that for a reversible process, no change occurs in
the total entropy produced, i.e., the entropy of the system plus the
entropy of the surroundings:
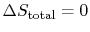 .
.
Figure 6.7:
Irreversible and reversible
state changes
|
|
We now carry out the same type of analysis for an irreversible
process, which takes the system between the same specified states as
in the reversible process. This is shown schematically in
Figure 6.7, with 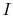 and
and
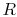 denoting the irreversible and reversible processes. In the
irreversible process, the system receives heat
denoting the irreversible and reversible processes. In the
irreversible process, the system receives heat 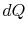 and does work
and does work
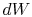 . The change in internal energy for the irreversible process is
. The change in internal energy for the irreversible process is
For the reversible process
Because the state change is the same in the two processes (we
specified that it was), the change in internal energy is the same.
Equating the changes in internal energy in the above two expressions
yields
The subscript ``actual'' refers to the actual process (which is
irreversible). The entropy change associated with the state change
is
![$\displaystyle dS = \frac{dQ_\textrm{actual}}{T} +\frac{1}{T}\biggl[dW_\textrm{rev} -dW_\textrm{actual}\biggr].$](img711.png) |
(6..3) |
If the process is not reversible, we obtain less work (see IAW
notes) than in a reversible process,
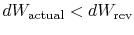 , so that for the irreversible process,
, so that for the irreversible process,
There is no equality between the entropy change 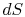 and the
quantity
and the
quantity 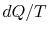 for an irreversible process. The equality is only
applicable for a reversible process.
for an irreversible process. The equality is only
applicable for a reversible process.
The change in entropy for any process that leads to a
transformation between an initial state ``a'' and a final state
``b'' is therefore
where
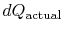 is the heat exchanged in the actual
process. The equality only applies to a reversible process.
is the heat exchanged in the actual
process. The equality only applies to a reversible process.
The difference
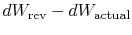 represents work
we could have obtained, but did not. It is referred to as lost work
and denoted by
represents work
we could have obtained, but did not. It is referred to as lost work
and denoted by
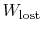 . In terms of this quantity we can
write,
. In terms of this quantity we can
write,
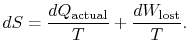 |
(6..4) |
The content of Equation (6.4) is that
the entropy of a system can be altered in two ways: (i) through heat
exchange and (ii) through irreversibilities. The lost work
(
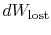 in Equation (6.4))
is always greater than zero, so the only way to decrease the entropy
of a system is through heat transfer.
in Equation (6.4))
is always greater than zero, so the only way to decrease the entropy
of a system is through heat transfer.
To apply the second law we consider the total entropy change (system
plus surroundings). If the surroundings are a reservoir at
temperature  , with which the system exchanges heat,
, with which the system exchanges heat,
The total entropy change is
The quantity (
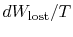 ) is the entropy generated due to
irreversibility.
) is the entropy generated due to
irreversibility.
Yet another way to state the distinction we are making is
 |
(6..5) |
The lost work is also called dissipation and noted 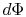 . Using
this notation, the infinitesimal entropy change of the system
becomes:
. Using
this notation, the infinitesimal entropy change of the system
becomes:
Equation (6.5) can also be written as a
rate equation,
 |
(6..6) |
Either of Equation (6.5) or
(6.6) can be interpreted to mean that the
entropy of the system, 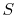 , is affected by two factors: the flow of
heat
, is affected by two factors: the flow of
heat 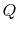 and the appearance of additional entropy, denoted by
and the appearance of additional entropy, denoted by
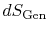 , due to irreversibility6.1. This additional entropy is zero when the
process is reversible and always positive when the process is
irreversible. Thus, one can say that the system develops
sources which create entropy during an irreversible process.
The second law asserts that sinks of entropy are impossible
in nature, which is a more graphic way of saying that
, due to irreversibility6.1. This additional entropy is zero when the
process is reversible and always positive when the process is
irreversible. Thus, one can say that the system develops
sources which create entropy during an irreversible process.
The second law asserts that sinks of entropy are impossible
in nature, which is a more graphic way of saying that
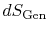 and
and
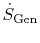 are positive definite
(always greater than zero), or zero in the special case of
reversible processes.
are positive definite
(always greater than zero), or zero in the special case of
reversible processes.
The term
which is associated with heat transfer to the system, can be
interpreted as a flux of entropy. The boundary is crossed by heat
and the ratio of this heat flux to temperature can be defined as a
flux of entropy. There are no restrictions on the sign of this
quantity, and we can say that this flux either contributes towards,
or drains away, the system's entropy. During a reversible process,
only this flux can affect the entropy of the system. This
terminology suggests that we interpret entropy as a kind of
weightless fluid, whose quantity is conserved (like that of matter)
during a reversible process. During an irreversible process,
however, this fluid is not conserved; it cannot disappear, but
rather is created by sources throughout the system. While this
interpretation should not be taken too literally, it provides an
easy mode of expression and is in the same category of concepts such
as those associated with the phrases ``flux of energy'' or ``sources
of heat.'' In fluid mechanics, for example, this graphic language is
very effective and there should be no objections to copying it in
thermodynamics.
Muddy Points
Do we ever see an absolute variable for entropy? So far, we have
worked with deltas only (MP 6.8)
I am confused as to
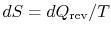 as opposed to
as opposed to
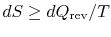 .(MP 6.9)
.(MP 6.9)
For irreversible processes, how can we calculate 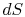 if not equal
to
if not equal
to 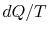 ?(MP 6.10)
?(MP 6.10)
UnifiedTP
|


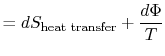
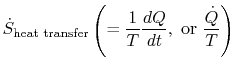
![]() as opposed to
as opposed to
![]() .(MP 6.9)
.(MP 6.9)
![]() if not equal
to
if not equal
to ![]() ?(MP 6.10)
?(MP 6.10)