8.7 Combined Cycles in Stationary Gas Turbine for Power Production
The turbine entry temperature in a gas turbine (Brayton) cycle is
considerably higher than the peak steam temperature. Depending on
the compression ratio of the gas turbine, the turbine exhaust
temperature may be high enough to permit efficient generation of
steam using the ``waste heat'' from the gas turbine. A configuration
such as this is known as a gas turbine-steam combined cycle power
plant. The cycle is illustrated in Figure 8.18.
Figure 8.18:
Gas turbine-steam combined cycle
[Kerrebrock, Aircraft Engines and Gas Turbines]
|
|
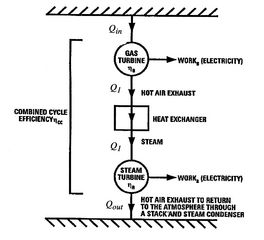
Figure 8.19:
Schematic of combined
cycle using gas turbine (Brayton cycle) and steam turbine (Rankine
cycle) [Langston]
|
|
The heat input to the combined cycle is the same as that for the gas
turbine, but the work output is larger (by the work of the Rankine
cycle steam turbine). A schematic of the overall heat engine, which
can be thought of as composed of an upper and a lower heat engine in
series, is given in Figure 8.19. The
upper engine is the gas turbine (Brayton cycle) which expels heat to
the lower engine, the steam turbine (Rankine cycle).
The overall efficiency of the combined cycle can be derived as
follows. We denote the heat received by the gas turbine as
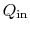 and the heat rejected to the atmosphere as
and the heat rejected to the atmosphere as
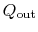 . The heat out of the gas turbine is denoted as
. The heat out of the gas turbine is denoted as
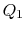 . The hot exhaust gases from the gas turbine pass through a
heat exchanger where they are used as the heat source for the
two-phase Rankine cycle, so that
. The hot exhaust gases from the gas turbine pass through a
heat exchanger where they are used as the heat source for the
two-phase Rankine cycle, so that 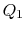 is also the heat input to the
steam cycle. The overall combined cycle efficiency is
is also the heat input to the
steam cycle. The overall combined cycle efficiency is
where the subscripts refer to combined cycle (CC), Brayton cycle (B)
and Rankine cycle (R) respectively.
From the first law, the overall efficiency can be expressed in terms
of the heat inputs and heat rejections of the two cycles as (using
the quantity 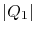 to denote the magnitude of the heat
transferred):
to denote the magnitude of the heat
transferred):
The first square bracket term on the right hand side is the Brayton
cycle efficiency, 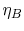 , the second is the Rankine cycle
efficiency,
, the second is the Rankine cycle
efficiency, 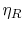 , and the term in parentheses is
, and the term in parentheses is
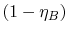 .
The combined cycle efficiency can thus be written as
.
The combined cycle efficiency can thus be written as
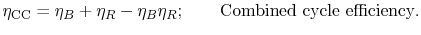 |
(8..5) |
Equation (8.5) gives insight into why
combined cycles are so successful. Suppose that the gas turbine
cycle has an efficiency of 40%, which is a representative value for
current Brayton cycle gas turbines, and the Rankine cycle has an
efficiency of 30%. The combined cycle efficiency would be 58%,
which is a very large increase over either of the two simple cycles.
Some representative efficiencies and power outputs for different
cycles are shown in Figure 8.20.
Figure 8.20:
Comparison of
efficiency and power output of various power products [Bartol
(1997)]
|
|
UnifiedTP
|


![]() and the heat rejected to the atmosphere as
and the heat rejected to the atmosphere as
![]() . The heat out of the gas turbine is denoted as
. The heat out of the gas turbine is denoted as
![]() . The hot exhaust gases from the gas turbine pass through a
heat exchanger where they are used as the heat source for the
two-phase Rankine cycle, so that
. The hot exhaust gases from the gas turbine pass through a
heat exchanger where they are used as the heat source for the
two-phase Rankine cycle, so that ![]() is also the heat input to the
steam cycle. The overall combined cycle efficiency is
is also the heat input to the
steam cycle. The overall combined cycle efficiency is
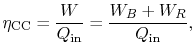
![]() to denote the magnitude of the heat
transferred):
to denote the magnitude of the heat
transferred):
![$\displaystyle \eta_\textrm{CC} = \frac{Q_\textrm{in} - \vert Q_1\vert +(\vert Q...
...out}}{\vert Q_1\vert}\right]
\left(\frac{\vert Q_1\vert}{Q_\textrm{in}}\right).$](img1181.png)