12.2 Conservation of Angular Momentum
[This section is excerpted from Fluid Flow: A First Course in
Fluid Mechanics, Macmillan Publishing Company, 1989.]
The momentum theorem developed in Chapter 10
gives the force acting on a fixed volume in terms of linear momentum
flux through the surface of the volume. In many situations we are
interested in the moment or torque on the volume. For this purpose
we may adapt the angular momentum law of mechanics to the flow of
fluids. Our starting point is the familiar law
where 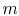 ,
, 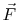 , and
, and 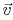 refer to a single particle. The
torque exerted by the force
refer to a single particle. The
torque exerted by the force 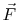 about a fixed point is
about a fixed point is
where 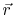 is the radius vector from the fixed point to the
point of application of
is the radius vector from the fixed point to the
point of application of 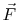 . The symbol,
. The symbol, 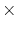 , signifies,
as usual, that the vector cross-product shall be taken. Then, from
Newton's law of motion,
, signifies,
as usual, that the vector cross-product shall be taken. Then, from
Newton's law of motion,
We now define a vector 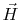 as the vector product of the radius
vector to the particle and the linear momentum, that is,
as the vector product of the radius
vector to the particle and the linear momentum, that is,
The quantity 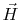 is called angular momentum. Upon
differentiating
is called angular momentum. Upon
differentiating 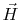 with respect to time, we find that
with respect to time, we find that
However,
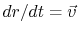 and the cross-product of a vector parallel
to itself is zero. The first term in the right-hand side therefore
vanishes and we have the result that
and the cross-product of a vector parallel
to itself is zero. The first term in the right-hand side therefore
vanishes and we have the result that
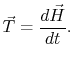 |
(12..1) |
Equation (12.1) states that the rate of change
of angular momentum of a particle about a fixed point is equal to
the torque applied to the particle.
We now seek to modify the law as expressed by
Equation (12.1) to be suitable for a fixed
volume. The torque on a material volume 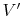 is
is
This is readily transformed into a control volume integral. We
have, therefore,
where
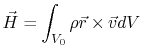 |
(12..2) |
is the angular momentum contained within the control volume.
Equation (12.2) represents the angular momentum
theorem. [For more information about angular momentum and
rotational energy, see pages 246 and 558 in Hibbeler's
Engineering Dynamics.]
UnifiedTP
|

