Banner

II.    Integral Momentum Theorem

We can learn a great deal about the overall behavior of propulsion systems using the integral form of the momentum equation.  The equation is the same as that used in fluid mechanics.

 

A.   An Expression of Newton's 2nd Law (e.g. = d/dt (mv))

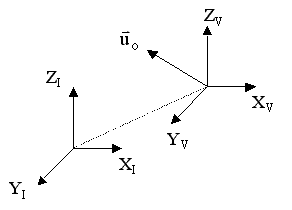Coordinate Frames1. Consider two coordinate systems:
a)  Inertial (labeled with subscript “I” in diagram at right)

b)  Fixed to vehicle (labeled with subscript “V” in diagram at right). Moves with velocity  relative to the inertial coordinate system. All velocities relative to the vehicle-fixed coordinate frame are denoted

2. Newton’s second law for a control volume of fixed mass

                  or

 

 

All external forces on control volume (pressure forces, shear forces, body forces)

  

Force due to change in inertia for accelerating vehicle

 

Change in momentum of mass in c.v.

To explain the above equation further, consider Figure 2.1

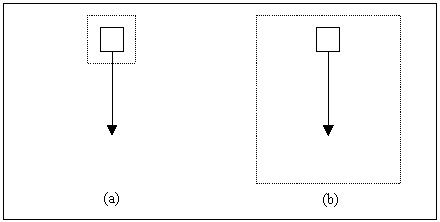
Falling Blocks

Figure 2.1 Falling blocks.

The falling block labeled (a) has a control volume fixed to it.  In this case, the first term on the right hand side of the above equation is nonzero since the control volume is accelerating relative to an inertial reference frame.  The second term is zero because the block is not accelerating relative to a coordinate system fixed to the control volume.  The opposite is true for the falling block labeled (b), which is falling within a fixed control volume.  The first term of the above equation is zero in this case because the control volume is not accelerating relative to an inertial reference frame.  The second term is nonzero because the block is moving relative to a coordinate system fixed to the control volume. The mathematical result of both cases is as follows,

 

(a)

 

(b)

 

As expected, the result is the same for both.  The integral momentum equation reduces to a familiar form, .

 

To continue, the equation can be rewritten as follows,

           

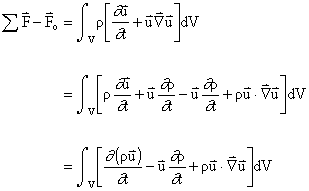
From conservation of mass,

           

so

           

NOTE: This is a vector equation.

3.  Considering only the components in the x-direction

           

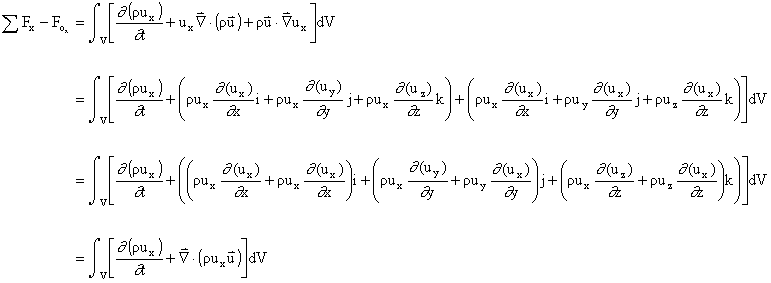
Then, by the divergence theorem,

                  where  is outward unit normal vector.

so

           

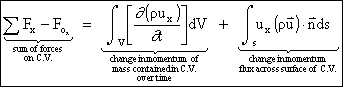
where the forces acting on the control volume may be composed of pressure forces, body forces, and skin friction

4. For steady flow, with no acceleration of the vehicle then

           

This is the form we will use most frequently in this class.

See a derivation of the integral form of the angular momentum equation - GO!

 

B. Application of the Integral Momentum Equation to Rockets

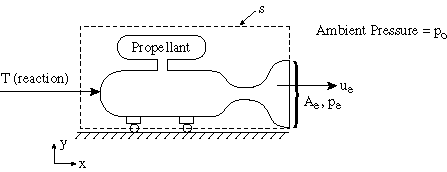
Rocket Momentum Theorem Diagram

Figure 2.2 Control volume for application of momentum theorem to a rocket.

     

     

                      Static thrust for a rocket engine

 

C. Application of the Momentum Equation to an Aircraft Engine

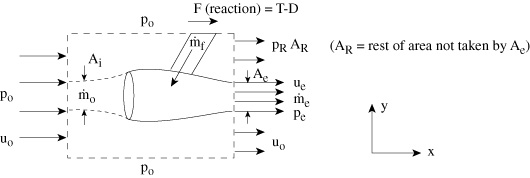
Aircraft Engine Momentum Theorem Diagram

Figure 2.3 Control volume for application of the momentum theorem to a gas turbine engine.

 

     

So we have:

     

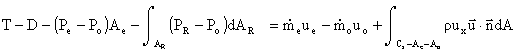
Everything that relates to flow through the engine is conventionally called thrust.  Everything that relates to the flow on the outside of the engine is conventionally call drag.  Therefore, gathering only those terms that relate to the fluid that passes through the engine, we have:

     

The thrust is largely composed of the net change in momentum of the air entering and leaving the engine, with a typically small adjustment for the differences in pressure between the inlet and the exit.  We could have arrived at the same equation by considering only the streamtube that passes through the engine as shown below:

Control Volume for Flow through an Engine

Figure 2.4 Control volume for flow through engine.

<< Previous Unified Propulsion Next >>