V.    Rocket Performance

A.   Thrust and Specific Impulse for Rockets

During the Fall semester thermodynamics lectures we used the steady flow energy equation to relate the exhaust velocity of a rocket motor to the conditions in the combustion chamber and the exit pressure

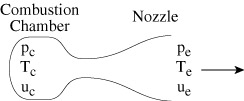
Figure 5.1 Schematic of rocket nozzle and combustion chamber

 

The steady flow energy equation

           

then with no heat transfer or shaft work

           

which can be written as

           

and manipulated to obtain

                                

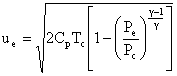
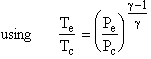
Then considering the relationship we derived for thrust

                         and assuming  p_e = p_o = 0

then     

and      

so        

Thus the specific impulse can be directly related to the exhaust velocity leaving the rocket

                      

B. The Rocket Equation

We can now look at the role of specific impulse in setting the performance of a rocket.  A large fraction (typically 90%) of the mass of a rocket is propellant, thus it is important to consider the change in mass of the vehicle as it accelerates.

                       

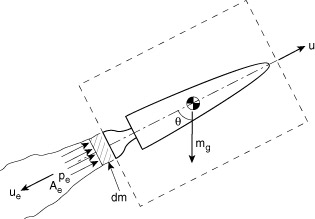
Figure 5.2 Schematic for application of the momentum theorem.

 

There are several ways to do this through applying conservation of momentum.  Here we will apply the momentum theorem differentially by considering a small mass, dm, expelled from the rocket during time dt.

The initial momentum of the mass in the control volume (the vehicle) is

                        m_vu

The final momentum of mass in the control volume (the vehicle and the mass expelled, dm) is

                        (m_v - dm)(u + du) + dm(u - u_e)

                         = m_vu + m_v du -  udm – dudm +udm -u_edm

The change in momentum during the interval dt is

                        = momentum_final – momentum_initial

           

                        = m_v du - u_edm  (since dudm is a higher order term)

Now consider the forces acting on the system which is composed of the masses m (the rocket), and dm (the small amount of propellant expelled from the rocket during time dt):

                       

Applying conservation of momentum, the resulting impulse, SFdt, must balance the change in momentum of the system.

                       

                       

then since              where  = propellant mass flow rate

we have

                       

or for p_e = p_o

                                          The Rocket Equation

The above can be integrated as a function of time to determine the velocity of the rocket.

If we set u_e = constant, and assume that at t=0, u=0, and neglect drag, and set q = 0, then we arrive at

                       

which can be integrated to give

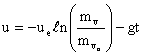                                                whereis the initial mass of the rocket

or

                       

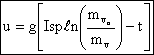
We can view this equation as being similar to the Breguet Range Equation for aircraft.  It presents the overall dependence of the principal performance parameter for a rocket (velocity, u), on the efficiency of the propulsion system (Isp), and the structural design (ratio of total mass to structural mass – since the initial mass is the fuel mass plus the structural mass and the final mass. is only the structural mass).

Assuming the rate of fuel consumption is constant, the mass of the rocket varies over time as

                                                

where t_b is the time at which all of the propellant is used.  This expression can be substituted into the equation for velocity and then integrated to find the height at the end of burnout:

                       

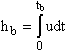
which for a single stage sounding rocket with no drag and constant gravity yields

                       

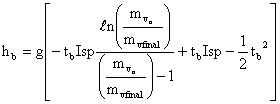
the final height of the rocket can then be determined by equating the kinetic energy of the vehicle at burnout with its change in potential energy between that point and the maximum height.  This is left as an exercise for the reader.

There is a great site on the web that describes performance analysis for multistage model rockets - GO!

 

Figure 5.3 The Saturn V rocket stood 365 feet tall and had 5 stages. It produced over 7.5 million pounds of thrust at liftoff (NASA, 1969).

 

<< Previous	Unified Propulsion	Next >>