15.4 First Law Analysis of Reacting Systems
The form of the first law for the control volume is (there is no
shaft work):
This is given in terms of the moles of the different constituents,
and it reduces to the more familiar form for a single fluid (say
air) with no reactions occurring. We need to specify one parameter
as the basis of the solution; 1 kmole of fuel, 1 kmole of air, 1
kmole total, etc. We use 1 kmole of fuel as the basic unit and
examine the burning of hydrogen.
The reactants and the products are both taken to be at
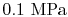 and
and
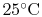 , so the inlet and exit
, so the inlet and exit 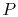 and
and 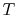 are specified. The control volume is the combustion chamber. There
is no shaft work done and the SFEE is in the form of
Equation (15.2). The enthalpy of the entering
gas is zero for both the hydrogen and the oxygen (elements have
enthalpies defined as zero at the reference state). If the exit
products are in the gaseous state, the exit enthalpy is therefore
related to the enthalpy of formation of the product by:
are specified. The control volume is the combustion chamber. There
is no shaft work done and the SFEE is in the form of
Equation (15.2). The enthalpy of the entering
gas is zero for both the hydrogen and the oxygen (elements have
enthalpies defined as zero at the reference state). If the exit
products are in the gaseous state, the exit enthalpy is therefore
related to the enthalpy of formation of the product by:
If the water is in a liquid state at the exit of the process:
There is more heat given up if the products emerge as liquid. The
difference between the two values is the enthalpy needed to turn the
liquid into gas at
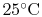 :
:
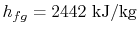 .
.
A more complex example is provided by the burning of methane
(natural gas) in oxygen, producing
The components in this reaction equation are three ideal gases
(methane, oxygen, and 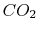 ) and liquid water. We again specify
that the inlet and exit states are at the reference conditions so
that:
) and liquid water. We again specify
that the inlet and exit states are at the reference conditions so
that:
Suppose the substances which comprise the reactants and the products
are not at
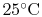 and
and
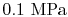 . If so, the
expression that connects the reactants and products is
. If so, the
expression that connects the reactants and products is
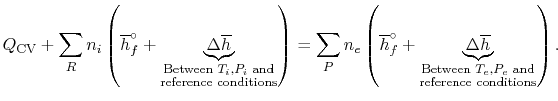 |
(15..4) |
Equation (15.4) shows that we must
compute the enthalpy difference
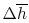 between the
reference conditions and the given state if the inlet or exit
conditions are not the reference pressure and temperature.
between the
reference conditions and the given state if the inlet or exit
conditions are not the reference pressure and temperature.
There are different levels of approximation for the computation:
- Assume the specific heat is constant over the range at some
average value,
- Use the polynomial expressions (Table A.6) in the
integral,
- Use tabulated values.
The first is the simplest and the crudest. Combustion processes
often involve changes of a thousand degrees or more and, as
Figure 15.2 shows, the specific heat
for some gases can change by a factor of two or more over this
range, although the changes for air are more modest. This means
that, depending on the accuracy desired, one may need to consider
the temperature dependence of the specific heat in computing
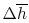 .
.
Figure 15.2:
Specific heat as a function
of temperature [from SB&VW]
|
|
Muddy Points
When doing cycle analysis, do we have to consider combustion
products and their effect on specific heat ratio (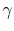 is not
1.4)? (MP 15.6)
is not
1.4)? (MP 15.6)
UnifiedTP
|


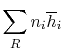
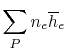
![]() and
and
![]() . If so, the
expression that connects the reactants and products is
. If so, the
expression that connects the reactants and products is
![]() is not
1.4)? (MP 15.6)
is not
1.4)? (MP 15.6)