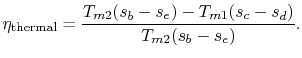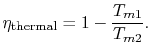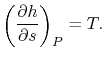8.5 Rankine Power Cycles
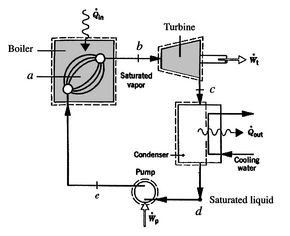
Figure 8.11:
Rankine power cycle with
two-phase working fluid [Moran and Shapiro, Fundamentals of
Engineering Thermodynamics]
|
|
A schematic of the components of a Rankine cycle is shown in
Figure 8.11. The cycle is shown on  -
-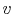 ,
,
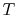 -
-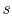 , and
, and 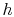 -
-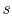 coordinates in Figure 8.12.
The processes in the Rankine cycle are as follows:
coordinates in Figure 8.12.
The processes in the Rankine cycle are as follows:
-
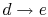 : Cold
liquid at initial temperature
: Cold
liquid at initial temperature 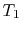 is pressurized reversibly to a
high pressure by a pump. In this process, the volume changes
slightly.
is pressurized reversibly to a
high pressure by a pump. In this process, the volume changes
slightly.
-
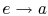 : Reversible constant pressure heating in a boiler to temperature
: Reversible constant pressure heating in a boiler to temperature
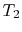 .
.
-
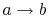 : Heat added at constant temperature
: Heat added at constant temperature 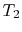 (constant
pressure), with transition of liquid to vapor.
(constant
pressure), with transition of liquid to vapor.
-
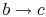 : Isentropic
expansion through a turbine. The quality decreases from unity at
point
: Isentropic
expansion through a turbine. The quality decreases from unity at
point 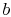 to
to 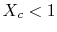 .
.
-
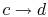 : Liquid-vapor mixture condensed at
temperature
: Liquid-vapor mixture condensed at
temperature 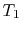 by extracting heat.
by extracting heat.
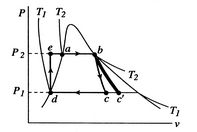
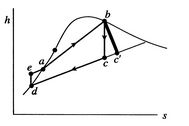
Figure 8.12:
Rankine cycle diagram.
Stations correspond to those in Figure 8.11
[ 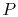
- 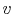
coordinates]
[ 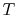
- 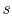
coordinates]
[ 
- 
coordinates]
|
In the Rankine cycle, the mean temperature at which heat is supplied
is less than the maximum temperature, 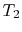 , so that the efficiency
is less than that of a Carnot cycle working between the same maximum
and minimum temperatures. The heat absorption takes place at
constant pressure over
, so that the efficiency
is less than that of a Carnot cycle working between the same maximum
and minimum temperatures. The heat absorption takes place at
constant pressure over 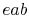 , but only the part
, but only the part 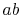 is isothermal.
The heat rejected occurs over
is isothermal.
The heat rejected occurs over 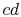 ; this is at both constant
temperature and pressure.
; this is at both constant
temperature and pressure.
To examine the efficiency of the Rankine cycle, we define a mean
effective temperature, 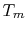 , in terms of the heat exchanged and the
entropy differences:
, in terms of the heat exchanged and the
entropy differences:
The thermal efficiency of the cycle is
The compression and expansion processes are isentropic, so the
entropy differences are related by
The thermal efficiency can be written in terms of the mean effective
temperatures as
For the Rankine cycle,
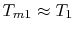 ,
,
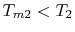 . From
this equation we see not only the reason that the cycle efficiency
is less than that of a Carnot cycle, but the direction to move in
terms of cycle design (increased
. From
this equation we see not only the reason that the cycle efficiency
is less than that of a Carnot cycle, but the direction to move in
terms of cycle design (increased 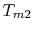 ) if we wish to increase
the efficiency.
) if we wish to increase
the efficiency.
There are several features that should be noted about
Figure 8.12 and the Rankine cycle in general:
- The
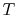 -
-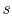 and the
and the 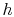 -
-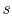 diagrams are not similar in shape, as they
were with the perfect gas with constant specific heats. The slope of
a constant pressure reversible heat addition line is, as derived in
Chapter 6,
diagrams are not similar in shape, as they
were with the perfect gas with constant specific heats. The slope of
a constant pressure reversible heat addition line is, as derived in
Chapter 6,
In the two-phase region, constant pressure means also constant
temperature, so the slope of the constant pressure heat addition
line is constant and the line is straight.
- The effect of
irreversibilities is represented by the dashed line from
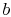 to
to
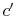 . Irreversible behavior during the expansion results in a value
of entropy
. Irreversible behavior during the expansion results in a value
of entropy 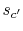 at the end state of the
at the end state of the 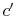 expansion that is
higher than
expansion that is
higher than 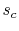 . The enthalpy at the end of the expansion (the
turbine exit) is thus higher for the irreversible process than for
the reversible process, and, as seen for the Brayton cycle, the
turbine work is thus lower in the irreversible case.
. The enthalpy at the end of the expansion (the
turbine exit) is thus higher for the irreversible process than for
the reversible process, and, as seen for the Brayton cycle, the
turbine work is thus lower in the irreversible case.
- The Rankine cycle
is less efficient than the Carnot cycle for given maximum and
minimum temperatures, but, as said earlier, it is more effective as
a practical power production device.
Muddy Points
Where does degrees Rankine come from? Related to Rankine cycles?
(MP 8.9)
UnifiedTP
|


 [
[ [
[
![]() , so that the efficiency
is less than that of a Carnot cycle working between the same maximum
and minimum temperatures. The heat absorption takes place at
constant pressure over
, so that the efficiency
is less than that of a Carnot cycle working between the same maximum
and minimum temperatures. The heat absorption takes place at
constant pressure over ![]() , but only the part
, but only the part ![]() is isothermal.
The heat rejected occurs over
is isothermal.
The heat rejected occurs over ![]() ; this is at both constant
temperature and pressure.
; this is at both constant
temperature and pressure.
![]() , in terms of the heat exchanged and the
entropy differences:
, in terms of the heat exchanged and the
entropy differences: