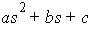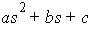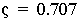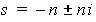Designing for a Specified Overshoot

Once you reduce this system, you will see it represents a second-order system. For a generic second-order system, the denominator will be of the form:

a, b, and c are functions of T, K and G.
The roots (poles) may be either real-value or complex, depending on the value of G.
When complex, the real-valued part of the pole-pair is always (clearly) just '-b'.
Then, as seen on the previous page, the decay envelope is identical for all complex-value solutions (and is determined by this real-valued part) .

To satisfy ZERO OVERSHOOT :

No overshoot requires NO IMAGINARY PARTS for the poles. They must be real-valued.
The fastest 'no overshoot' response is obtained by making the 'dominant pole' as fast as possible.
So, of all real-valued solutions possible, we want to pick 'G' such that both poles are at the same location.
(Otherwise, with any other real-valued solutions where the poles are in different locations, one of the poles is faster, while the other is slower.)

To satisfy 5% OVERSHOOT, we can use two approaches:

Quick approach : We can recall that
results in about a 5 % overshoot, and that this corresponds to having real and imaginary parts of identical magnitude:

More thorough analysis : Solve for the location of the 'first hit' on the decay envelope.

For instance, say we wish to solve for the imaginary components of the pole-pair that would result in 50% overshoot.
The real-value part is fixed for all complex solutions, as we've seen.

Step 1. Determine the time required for the [upper] first-order envelope to reach (1+0.5) times the final value. (This is identical with the time required for the lower envelope to reach (1-0.5) times the final value.)
Solve explicitly for the number of time constants required:
Multiply N_tau * tau to get the time required for a half-cycle (pi rad from min peak to max).
Solve for the imaginary solution (frequency) to the required roots for this performance spec.
For 5% overshoot, the solution is
which is very close to the solution we got for zeta=0.707:
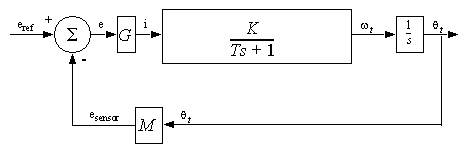
Now, just solve for G, given this desired imaginary solution.

gonzo@mit.edu

page 5 (of 10)

2.010 Tutorial #7, 5-Nov-00