Slide Rule
QUESTIONS OR COMMENTS
	AUTHOR:	Liyen Liang
	E-MAIL:	lliang@mit.edu
	COURSE:	2
	CLASS/YEAR:	4

MAIN FUNCTIONAL REQUIREMENT:  Perform simple mathematical functions

DESIGN PARAMETER:  Sliding mechanical ruler

GEOMETRY/STRUCTURE:

This is a picture of a basic beginner’s slide rule for various math operations including mutiplication/division and square/squareroot:

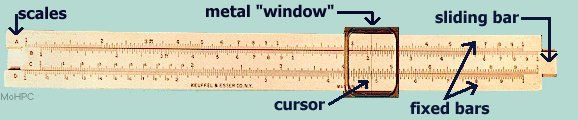Components of A Slide Rule Also See As VRML (lets you walk around, zoom in/out around a 3D model)

The slide rule is actually made of three bars that are fixed together. The sliding center bar is sandwiched by the outer bars which are fixed with respect to each other. The metal "window" is inserted over the slide rule to act as a place holder. A cursor is fixed in the center of the "window" to allow for accurate readings.

The scales (A-D) are labeled on the left-hand side of the slide rule. The number of scales on a slide rule vary depending on the number of mathematical functions the slide rule can perform. Multiplication and division are performed using the C and D scales. Square and square root are performed with the A and B scales. The numbers are marked according to a logarithmic scale. Therefore, the first number on the slide rule scale (also called the index) is 1 because the log of zero is one.

EXPLANATION OF HOW IT WORKS/ IS USED:

1. Move the sliding middle section with scale "C" so that the 1 on the scale matches the 3 on the lower fixed section with scale "D".
2. Now read along the top scale to the 2 and see what it says on the bottom scale.
3. The bottom scale should read approximately 6 which is the answer.
4. We have just added a log of 3 distance on the bottom to a log of 2 distance on the top to get a log of 6 distance on the bottom.

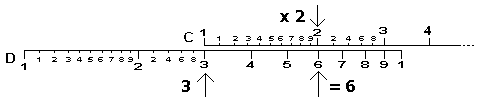Calculating 3 x 2 on a Slide Rule

The slide rule also works for numbers larger than what is represented on the scale of the ruler. For example, double digit numbers can be represented by mentally "moving" the decimal places.

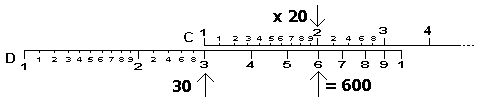Calculating 30 x 20 on a Slide Rule

1. Set the divisor on the C scale opposite the dividend on the D scale
2. Read the result of the D scale under the C scale index (where the scale reads 1)

1. Perform the multiplication method for the first two factors as previous described.
2. Then move the C index to the previous product to start the next multiplication. The hairline or cursor was handy for keeping a pointer on the previous product while moving the slide.

To find the square root of a number:

1. The A and B scales are the squares of the D and C scales, respectively. Example: To determine the square root of 9, look on the A scale for 9.
2. Find the answer, 3, on the D scale below the A scale.

To find the square:

1. Reverse the square root process to find the square.

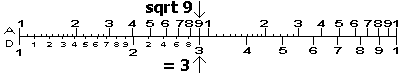Calculating 91/2

IMPORTANT NOTE: There may be confusion about which side of the A scale to use. For example, the square root of 4 is 2 and the square root of 400 is 20 - both calculations can be found using the left side of the A scale. However, to find the square root of 40, it is necessary to use the right side of the scale to get the correct answer of ~6.3. The simplest method to determine which side of the A scale to use is to write the number in standard scientific notation form (ie n.nnn x 10^exp). If the power of ten was even (exp = even), use the left side to find the square/square root (and the resulting exponent of ten was one half the original exponent). For odd powers of ten, shift the decimal place of the number one place to the right and decreased the exponent of ten by one. Then use the right side (and again used one half the exponent of ten for the resulting exponent).

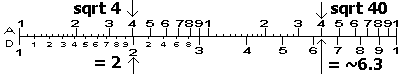Title

DOMINANT MATHEMATICS:

In 1614, John Napier discovered the logarithm (reference: HP Computer Museum webpage)

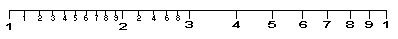Title

Reference: The System Source Computer Museum: Mechanical Calculators   (http://www.syssrc.com/museum/mechcalc/javaslide/srinst.html)

Notice that on this scale the distance between the divisions is decreasing. This is a characteristic of a log scale. A logarithm relates one number to another number much like a mathematical function. The log of a number, to the base 10, is defined by:

(1)

The "magic" of the slide rule is actually based on a mathematical logarithmic relation:

(2)

(3)

These relations made it possible to perform multiplication and division using addition and subtraction. Before the slide rule, the product of two numbers were found by looking up their respective logs and adding them together, then finding the number whose log is the sum, also called the inverse log.

(4)

Equation (4) can be found by manipulating equation (2). It demonstrates that a square of a number can be found by doubling its log and getting the inverse log of the answer. Therefore, scales A and B were developed to perform the square and square root functions on the slide rule. The A scale is just twice the D scale on the same printed on the same length of the slide rule as the D scale.

The slide rule made its first appearance in the late 17^th century. The slide rule made it easier to utilize the log relations by developing a number line on which the displacement of the numbers were proportional to their logs. The slide rule eased the addition of the two logarithmic displacements of the numbers, thus assisting with multiplication and division in calculations. More functionality was later added such as the ability to compute exponential and trigonometric functions. Slide rules come in many different styles, including sliding bars and rotating cylinders and circles.

LIMITING PHYSICS:

The accuracy of the calculations made with a slide rule depends on the accuracy with which the user can read the numbers off the scale. More divisions allow for more decimal places which means increased accuracy.

PLOTS/GRAPHS/TABLES:

None Submitteed

WHERE TO FIND SLIDE RULES:

Slide rules are rarely used because of the advent of electronic calculators and computers. However, they are a valuable educational tool because of the mathematics behind its design. Also, unlike electronic calculators, the slide rule helps the user develop a "feel" for numbers.

REFERENCES/MORE INFORMATION:

To learn more about slide rules (different types, more scales, etc.), go to: http://www.hpmuseum.org/srinst.htm

To buy or trade slide rules get great slide rule links, go to:   http://www.comcen.com.au/~adavie/slide/

To download slide rule software for Windows:  http://www.comcen.com.au/~adavie/slide/download.html

Try using a slide rule! - Interactive Java slide rule  http://www.comcen.com.au/~adavie/javaslide/javaslide.html