 |
 |
| VIOLIN | ||
| QUESTIONS OR COMMENTS | ||
 |
AUTHOR: | Gina Kim |
| E-MAIL: | kimna@MIT.EDU | |
| COURSE: | Undecided | |
| CLASS/YEAR: | 1 | |
MAIN FUNCTIONAL REQUIREMENT: Create and Resonate (Hopefully Pleasant) Sound Waves
DESIGN PARAMETER: Simple harmonic oscillator (in the form of a violin, of course)
GEOMETRY/STRUCTURE:
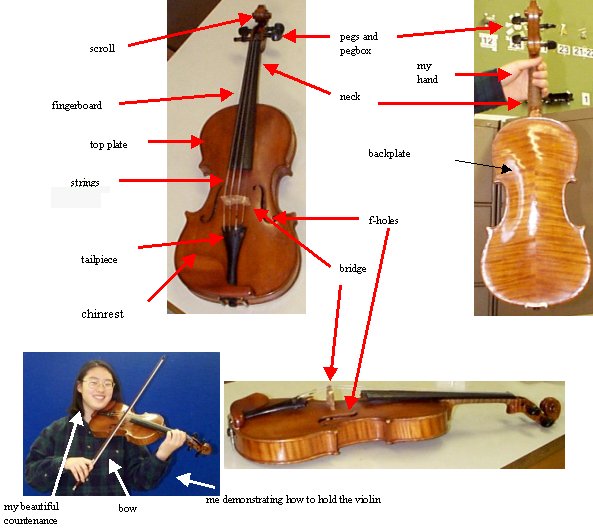 |
| Figure 0: Major Components of A Violin |
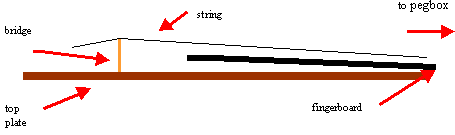 |
| Figure 1: Schematic of Violin Model Components |
EXPLANATION OF HOW IT WORKS/ IS USED:
Okay, some basics. It’s pretty obvious that the source of the sound in a violin has something to do with the strings and the body, which resonates the sound made by the strings. The idea is that by plucking, bowing, or hitting a string, a violinist can make it vibrate. (Hitting is fairly rare, but it can be done; in one bowing stroke, col legno, you do hit the string with the wooden part of the bow.) In this paper, I will concentrate on the plucking, because the physics for bowing and hitting are similar. The vibration resonated from the string and the body excites the air molecules around the violin, creating a wave that we perceive as sound.
DOMINANT PHYSICS:
The String
The vibration (and therefore the sound) is affected by three main variables:
- The tension of the string. At the end of the violin is the pegbox, where the pegs are (duh!). The strings are wound around the peg, and so the tension in the string can be changed when the pegs are loosened or tightened.
- The more tension, the higher the frequency of the vibration (and therefore, the higher the pitch).
- The length of the string. While the length of all of the strings on a violin are about the same, the actual length of the vibrating part can be changed, by putting one’s fingers down and making the string length effectively shorter. Another way that we can see how string length changes the sound is through comparisons with other stringed instruments: the length of the strings on a viola are longer than those on a violin, so we would expect a lower sound. And that is precisely how it is.
- The shorter the length of the string, the higher the frequency.
- The mass per unit length. This really isn’t a true variable, because a violinist can’t actually change it. In plain English, the "mass per unit length" is just how thick the strings are. On a violin, the E-string is thinner than the A-string, and that’s just how it is; no amount of wishing will cause it to be otherwise. However, an A-string on a cello will be much thicker, causing a lower sound. (Actually, that isn’t the only reason; the two variables described above also play a part.)
- The thinner the string, the higher the frequency.
The Body
No, I’m not talking about the new governor from Minnesota (my home state, by the way), I’m talking about the rest of the violin. Think about it: have you ever played with an electric guitar when the amplifier is off? Plucking the strings only gives off a rather pathetic twang. Because the vibration caused by plucking a string is relatively "small," not very many air molecules are excited. What we need, therefore, is something that can act as a resonator.
The strings rest on the bridge, which transfers the vibrations down to the body of the instrument. The violin resonates in two main ways:
- The top and back plate. These plates radiate most of the sound.
- Air circulating within the violin. This resonance is not nearly as important as the one mentioned above.
Modes ‘n’ Nodes
| Variable | Description | Metric Units | English Units |
| m | mode | -- | -- |
| n | node | -- | -- |
| L | Length of string | m | ft |
| D | Distance from the site of the plucking to the bridge | m | ft |
| T | Tension | N (kg m s-2) | lbf |
| M | Mass per unit string length | kg m-1 | lb ft-1 |
| v | velocity | m s -1 | ft s-1 |
| F | frequency | Hz (s-1) | Hz (s-1) |
| l | wavelength | m | ft |
Instruments have very separate, distinct sounds, called "timbres" in music lingo. When you listen to the radio or go to the symphony, it is usually easy to pick out the various instruments, since an oboe (hopefully) sounds nothing like a tuba. These different timbres are caused by harmonics. Each instrument has a specific pattern of harmonics, which create the unique sound. In this section, I will try to explain how a violin’s harmonics are created.
Have you ever seen the high school physics demonstration where the teacher gets someone to hold one end of a rope and then frantically waves the other end up and down? In the middle of the rope, if the demonstration goes well, you can see a "node," which is a point on the string which doesn’t move. Sometimes, by waving even more frantically (i.e. higher frequency), the teacher can create three or four nodes.
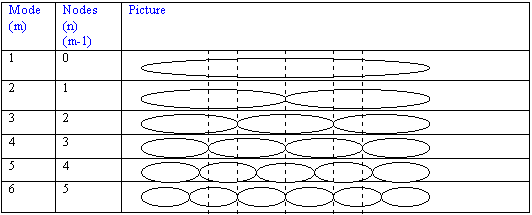 |
| Figure 2: Relation Between Nodes and Modes |
You may very well be wondering, "well, what does all this have to do with the violin?" Well, a violin string works on the same sort of principle. Because it is vibrating so fast (the frequency is high), many nodes can be created (See Figure 2 above).
When a string is plucked in the middle, all of the even modes will be still (See Figure), while all of the odd modes will oscillate furiously. However, this isn’t what usually happens when one plays the violin: usually, the string is played close to one end. In this case, some modes will be more excited than others. We can find which modes are completely still, by using an equation with a pretty interesting relationship:
Non-Excited Modes = m (L / D) ( Equation 1)Ta-dah! This relationship is important because of how modes are related to sound; the equation tells us which modes don’t vibrate (and therefore, which do). The excited modes give off distinct frequencies, and the combination of which frequencies are present and to what extent they are present (their amplitude) gives the distinct timbre of the violin. The equation for the frequency is given by:
fn = (n / 2L) (T / M)1/2 (Equation 2)
This equation is just a glorified version of the standing wave equation:
fn = (nv / 2L) (Equation 3)
Derivation: f = v/l l = 2L (the wavelength is 2L because the wave travels up and back down the string) fn = (nv / 2L) v=(T/M)1/2 (the units work out: ( (kg m s-2) / (kg m-1 ) )1/2 = m s-1 ) fn = (n / 2L) (T / M)1/2
Anyway, a given note on a violin will have several frequencies vibrating at once. This distinct combination creates the uniquely beautiful timbre of the violin.
LIMITING PHYSICS:
Ideally, the violin string doesn’t move, the material is constant throughout, and it has no bending stiffness. However, we know that this is impossible, given the inconsistent quality of natural materials. (Although it is interesting to note that most violinists prefer to use gut strings, not synthetic ones, showing that sometimes nature does know what it’s doing.) More interesting are debates on how the body of the violin affects the resonance capabilities. If, for instance, a violin’s top plate is too thick, the sound will be muted. If it is too thin, the sound will be "boomy." But we all know that the most limiting factor of how good a violin sounds is simply the level of the person playing.
PLOTS/GRAPHS/TABLES:
None Submitted
WHERE TO FIND VIOLINS:
Well, I’d just check out your local symphony orchestra. Especially if you’re around the MIT area, you could check out the MIT Symphony, of which I’m a member (I know, gratuitous plug). Or you could try going to your neighborhood violin shop to take a look around.
REFERENCES/MORE INFORMATION:
Cremer, Lothar. The Physics of the Violin. John S. Allen, trans. Cambridge: MIT, 1984.
Howard, David M. and Angus, James. Acoustics and Psychoacoustics. Oxford: Focal, 1996.