



Lecture 8
Example Problem
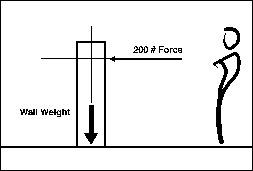
A Force on the Wall
Given:
a 200 pound force is applied to a masonry or stone wall.
Determine:
a)the stability of the wall. b) if a 100 pound force can be resisted by the wall. c) the required density of the wlal materials for eh wall to resist the 200 pound thrust. Note: Oringinal image scale was 1" = 100 lb.
Solution:
the first thing to do with any graphical problem is to examine the given forces for points of concurrence. In this case the point lies along the line of action of the lateral thrust. The self-weight load of the wall must be translated vertically along the line of action of the weight until the heads of both forces are together. Now both forces must be drawn to an approprite scale.
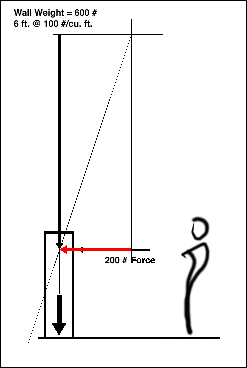
Both vectors now meet head to head and are drawn according to scale. The next step is to determine the resultant of the two vectors. IF the resultant passes within the middle third of the structure, then gravity and self-weight alone will provide the means to resist the thrust. If this is not the case then the load must be reduced OR the weight of the wall must be increased. The line of action of the resultant clearly passes outside of the boundries of the wall.
Could the geometry of the wall be altered so that the thrust could be resisted with only a 600 pound wall? If so, what would be the shape of the wall? How many alternatives can be found for this solution? Are any of the shapes familiar?
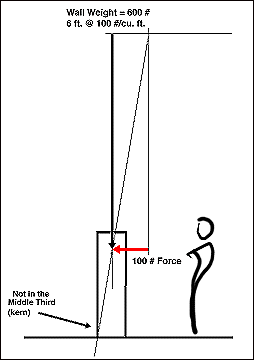
If the load is reduced to 100 pounds the resulting vector still passes outside of the middle third of the structure.
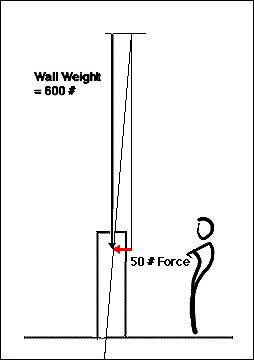
Only when the load is reduced to approximatly 50 pounds does the resultant vector finally pass through the middle third of this wall. This illustrates why so many large retaining walls which must resist great loads are tapered. They reflect the adaptation of the wall geometry to the path of the resultant.
Copyright © 1997 by Chris Luebkeman











