

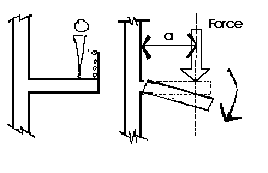
 The Moment of a force
is a measure of its tendency to cause a body to rotate about a specific
point or axis. This is different from the tendency for a body to move, or
translate, in the direction of the force. In order for a moment to develop,
the force must act upon the body in such a manner that the body would begin
to twist. This occurs every time a force is applied so that it does not
pass through the centroid of the body. A moment is due to a force not having
an equal and opposite force directly along it's line of action.
The Moment of a force
is a measure of its tendency to cause a body to rotate about a specific
point or axis. This is different from the tendency for a body to move, or
translate, in the direction of the force. In order for a moment to develop,
the force must act upon the body in such a manner that the body would begin
to twist. This occurs every time a force is applied so that it does not
pass through the centroid of the body. A moment is due to a force not having
an equal and opposite force directly along it's line of action.
Imagine two people pushing on a door at the doorknob from opposite sides.
If both of them are pushing with an equal force then there is a state of
equilibrium. If one of them would suddenly jump back from the door, the
push of the other person would no longer have any opposition and the door
would swing away. The person who was still pushing on the door created a
moment.
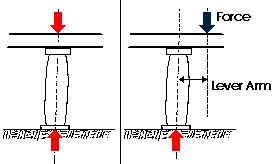
The magnitude of the moment of a force acting about a point or axis is
directly proportinoal to the distance of the force from the point or axis.
It is defined as the product of the force (F) and the moment arm (d). The
moment arm or lever arm is the perpendicular distance between
the line of action of the force and the center of moments.
Moment = Force x Distance or M = (F)(d)
The Center of Moments may be the actual point about which the
force causes rotation. It may also be a reference point or axis about which
the force may be considered as causing rotation. It does not matter as long
as a specific point is always taken as the reference point. The latter case
is much more common situation in structural design problems.
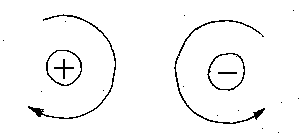 A moment is expressed in units of foot-pounds, kip-feet,
newton-meters, or kilonewton-meters. A moment also has a sense; A clockwise
rotation about the center of moments will be considered a positive moment;
while a counter-clockwise rotation about the center of moments will be considered
negative. The most common way to express a moment is
A moment is expressed in units of foot-pounds, kip-feet,
newton-meters, or kilonewton-meters. A moment also has a sense; A clockwise
rotation about the center of moments will be considered a positive moment;
while a counter-clockwise rotation about the center of moments will be considered
negative. The most common way to express a moment is
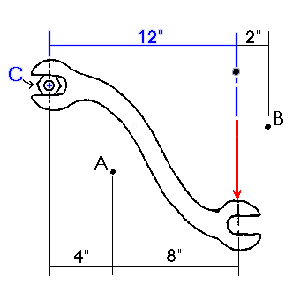
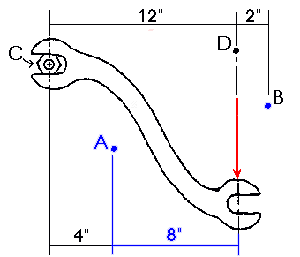
Moment about C
The moment arm for calculating the moment around point C is 12 inches. The
magnitude of the moment about point C is 12 inches multiplied by the force
of 100 lbs to give a total moment of 1200 inch-lbs (or 100 ft-lbs).
Moment Arm (d) = 12 inches
Magnitude (F) = 100 lbs
Moment = M = 100 lbs x 12 in. = 1200 in-lbs
Similarly, we can find the moments about any point in space.
| Moment @ | A | B | D |
| Moment Arm | 8 inches | 2 inches | 0 inches |
| Magnitude of F | 100 pounds | 100 pounds | 100 pounds |
| Total Moment | 800 in- pounds | 200 in- pounds | 0 in- pounds |
 |
 |
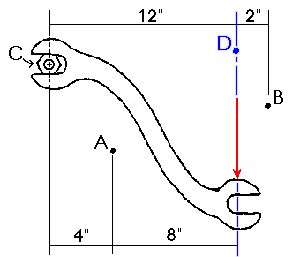 |
A moment causes a rotation about a point or axis. If the moment is to be taken about a point due to a force F, then in order for a moment to develop, the line of action cannot pass through that point. If the line of action does go through that point, the moment is zero because the magnitude of the moment arm is zero. Such was the case for point D in the previous wrench poblem. The total moment was zero because the moment arm was zero as well.
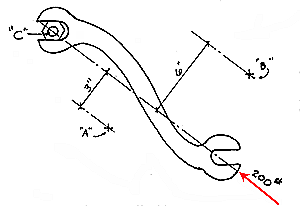
As another example, let us assume that 200 pound force is applied to the
wrench as indicated. The moment of the 200 pound force applied at C is zero
because:
M = F x d = 200 lbs x 0 in = 0 in-lbs
In other words, there is no tendency for the 200 pound force to cause the wrench to rotate the nut. One could increase the magnitude of the force until the bolt finally broke off (shear failure).
The moment about points X, Y, and Z would also be zero because they also
lie on the line of action.
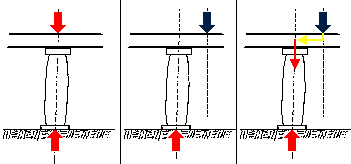
A moment can also be considered to be the result of forces detouring from
a direct line drawn between the point of loading of a system and its supports.
In this case, the blue force is an eccentric force. In order for it to reach
the base of the column, it must make a detour through the beam. The greater
the detour, the greater the moment. The most efficient structural systems
have the least amount of detours possible. This will be discussed in more
detail in Lecture 37 and
later courses.
There are cases in which it is easier to calculate the moments of the componenets of a force around a certain point than it is to calculate the moment of the force itself. It could be that the determination of the perpendicular distance of the force is more difficult than determining the perpendicular distance of components of the force. The moment of several forces about a point is simply the algebraic sum of their component moments about the same point. When adding the moments of componenets, one must take great care to be consistant with the sense of each moment. It is often prudent to note the sense next to the moment when undertaking such problems.
![]() Combined
Moments
Combined
Moments
![]() Moments
on a Beam
Moments
on a Beam
Frequently Asked Questions
Any difficulty with calculating a moment can usually be traced to one of
the following:
Questions For Thought
What is the moment about point B and about point D for both of the cases
shown in the wrench example above? How could adding an extension to the
end of the wrench help turn a rusted bolt? What kind of structural systems
would have the least number of "detours?"
Problems
Associated Readings
Shaeffer, R.E. Elementary Structures for Architects and Builders. pp. 33-39.