The circuit with theoretical conservation theorem (11.0.8) equates the
power flowing into the circuit to the rate of change of the energy
stored and the rate of energy dissipation. In a field, theoretical
generalization, the energy must be imagined distributed through space
with an energy density W (joules/m3), and the power is dissipated
at a local rate of dissipation per unit volume Pd (watts/m3).
The power flows with a density S (watts/m2), a vector, so that
the power crossing a surface Sa is given by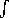 
Sa S
da
. With these field-theoretical generalizations, the power
flowing into a volume V, enclosed by the surface S must be given
by
where the minus sign takes care of the fact that the term on the left
is the power flowing into the volume.
According to the right-hand side of this equation, this input power is
equal to the rate of increase of the total energy stored plus the
power dissipation. The total energy is expressed as an integral over
the volume of an energy density, W. Similarly,
the total power dissipation is the integral over the volume of a
power dissipation density Pd.
Figure 11.1.1 Integral form of energy
conservation theorem applies to system within arbitrary volume V
enclosed by surface S.
The volume is taken as being fixed, so the time derivative can be
taken inside the volume integration on the right in (1). With the
use of Gauss' theorem, the surface integral on the left is then
converted to one over the volume and the term transferred to the
right-hand side.
Because V is arbitrary, the integrand must be zero and a
differential statement of energy conservation follows.
With an appropriate definition of S, W and Pd, (1) and
(3) could describe the flow, storage, and dissipation not only of
electromagnetic energy, but of thermal, elastic, or fluid mechanical
energy as well. In the next section we will use Maxwell's equations
to determine these variables for an electromagnetic system.
