| |
Introduction
|
| 11.0.1* |
A capacitor C, an inductor L, and a resistor R are in series,
driven by the voltage v(t) and carrying the current i(t). With
vc defined as the voltage across the capacitor, show that vi =
dw/dt + i2 R where w =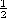 C vc2 + C vc2 + 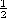 Li2.
Argue that w
is the energy stored in the inductor and capacitor, while i2 R is
the power dissipated in the resistor. Li2.
Argue that w
is the energy stored in the inductor and capacitor, while i2 R is
the power dissipated in the resistor. |
| | Integral and Differential Conservation Statements |
|---|
| 11.1.1* | Consider a system in which the fields are y and/or z directed and
independent of y and z.
Then S = Sx (x, t)ix, W = W(x, t), and Pd = Pd(x, t).
| (a) | Show that for a volume having area A in any y - z plane
and located
between x = x1 and x = x2, (1) becomes

|
| (b) | Take the limit where x1 - x2 = 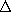 x x 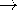 0 and
show that the one-dimensional form of (3) results. 0 and
show that the one-dimensional form of (3) results.
|
| (c) | Based on (a), argue that Sx is the power flux density
in the x direction.
|
|
| | Poynting's Theorem |
|---|
| 11.2.1* | The perfectly conducting plane parallel electrodes of Fig.
13.1.1 are driven at the left by a voltage source Vd (t) and are
"open circuit" at the right, as shown in Fig. 13.1.4. The system
is EQS.
|
| 11.2.2 | The perfectly conducting plane parallel electrodes of Fig. 13.1.1
are driven at the left by a current source Id(t), as shown in Fig.
13.1.3. The system is MQS.
| (a) | Determine S.
|
| (b) | From S, find the input power.
|
| (c) | Evaluate the right-hand side of (11.1.1) for a volume
enclosing the region between the electrodes, and show that if the
electric energy
storage is neglected, it is indeed equal to the left-hand side.
|
| (d) | Under what conditions is the electric energy storage
negligible?
|
|
| | Ohmic Conductors with Linear Polarization and Magnetization |
|---|
| 11.3.1* | In Example 7.3.2, a three-dimensional dipole current source
drives circulating currents through a uniformly conducting material.
This source is so slowly varying with time that time rates of change
have a negligible effect. Consider first the power flow as pictured
in terms of the Poynting flux density, (3).
| (a) | Show that

|
| (b) | Show that

|
| (c) | Using these results, show that (11.1.3) is indeed
satisfied.
|
| (d) | Now, using the alternative EQS power theorem, evaluate
S as given by (23) and again show that (11.1.3) is satisfied.
|
| (e) | Observe that the latter evaluation is much simpler to carry
out and that the latter power flux density is easier to picture.
|
|
| 11.3.2 | Coaxial perfectly conducting circular cylindrical electrodes make
contact with a uniformly conducting material of conductivity  in the annulus b < r <
a, as shown in Fig. P11.3.2. The length l is large compared to
a. A voltage source v drives the system at the left, while the
electrodes are "open" at the right. Assume that v(t) is so slowly
varying that the voltage can be regarded as independent of z.
in the annulus b < r <
a, as shown in Fig. P11.3.2. The length l is large compared to
a. A voltage source v drives the system at the left, while the
electrodes are "open" at the right. Assume that v(t) is so slowly
varying that the voltage can be regarded as independent of z.
 Figure P11.3.2
Figure P11.3.2
| (a) | Determine E, 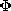 , and H
in the annulus. , and H
in the annulus.
|
| (b) | Evaluate the Poynting power flux density
S [as given by (3)] in the annulus.
|
| (c) | Use S to evaluate the total power dissipation by
integration over the surface enclosing the annulus.
|
| (d) | Show that the same result is
obtained by integrating Pd over the volume.
|
| (e) | Evaluate S as given by (23), and use that
distribution of the power flux density to determine the total power
dissipation.
|
| (f) | Make sketches of
the alternative distributions of S.
|
| (g) | Show that the input power
is vi, where i is the total current from the voltage source.
|
|
| 11.3.3* | A pair of perfectly conducting circular plates having a spacing d
form parallel electrodes in a system having cylindrical symmetry
about the z axis
and the cross-section shown by Fig. P11.3.3. The central region
between the plates is filled out to the radius b by a uniformly
conducting material having conductivity  and uniform permittivity and uniform permittivity
 , while the surrounding region, where b < r < a, is free space. A
distributed voltage source v(t) constrains the potential difference
between the outer edges of the electrodes. Assume that the system is EQS. , while the surrounding region, where b < r < a, is free space. A
distributed voltage source v(t) constrains the potential difference
between the outer edges of the electrodes. Assume that the system is EQS.
|
| 11.3.4 | In Example 7.5.1, the steady current distribution in and around a
conducting circular cylindrical rod immersed in a conducting material
was determined. Assume that Eo is so slowly varying that it can be
regarded as static.
| (a) | Determine the distribution of Poynting power
flux density S, as given by (3).
|
| (b) | Determine the alternative S given by (23).
|
| (c) | Find the power dissipation
density Pd in and around the rod.
|
| (d) | Show that the differential
energy conservation law [(11.1.3) with 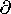 W/ W/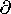 t = 0]
is satisfied at each point in and around the rod using either of
these distributions of S. t = 0]
is satisfied at each point in and around the rod using either of
these distributions of S.
|
|
| | Energy Storage |
|---|
| 11.4.1* | In Example 8.5.1, the inductance L of a spherically shaped coil
was found by "adding up" the flux linkages of the individual windings.
Taking an alternative approach to finding L, use the fields found in
that example to determine the total energy storage, wm. Then use
the fact that wm = 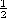 Li2 to show that L is as given by
(8.5.20). Li2 to show that L is as given by
(8.5.20).
|
| 11.4.2 | In Prob. 9.6.3, a coil has turns at the interface between a
magnetizable material and a circular cylindrical core of free space,
as shown in Fig. P9.6.3. Assume that the system has a length l in
the z direction and determine the total energy, wm. (Assume that
the rotatable coil carries no current.) Use the fact that wm =
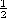 L i2 to find L. L i2 to find L.
|
| 11.4.3* | In Example 8.6.4, the fields of a coil distributed throughout a
volume were found. Using these fields to evaluate the total energy
storage, show that the inductance is as given by (8.6.35).
|
| 11.4.4 | The magnetic circuit described in Prob. 9.7.5 and shown in Fig.
P9.7.5 has two electrical excitations. Determine the total magnetic
coenergy, w'm (i1, i2, x).
|
| 11.4.5 | The cross-section of a motor or generator is shown in Fig.
11.7.7.
| (a) | Determine the magnetic coenergy density Wm', and hence
the total coenergy wm'.
|
| (b) | By writing wm' in the form of
(11.4.24), determine L11, L12, and L22.
|
|
| 11.4.6* | The material in the system of Fig. 11.4.3 has the constitutive
law of (28). Show that the total coenergy is

|
| 11.4.7 | Consider the system shown in Fig. P9.5.1 but with  a = a =  o and
the region where B = o and
the region where B =  b H now
filled with a material having the constitutive law b H now
filled with a material having the constitutive law

| (a) | Determine B and H in each region.
|
| (b) | Find the coenergy
density in each region and hence the total coenergy wm' as a
function of the driving current i.
|
|
| | Electromagnetic Dissipation |
|---|
| 11.5.1* | In Example 7.9.2, the Maxwell capacitor has an area A
(perpendicular to x), and the terminals are driven by a source v =
Re [ exp (j exp (j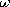 t)]. The sinusoidal steady state has been
established. Show that the time average power dissipation in the
lossy dielectrics is t)]. The sinusoidal steady state has been
established. Show that the time average power dissipation in the
lossy dielectrics is

|
| 11.5.2 | In Example 7.9.3, the potential is found in the EQS approximation
in and around a lossy dielectric sphere embedded in a lossy dielectric
and stressed by a uniform field having a sinusoidal dependence on time
(7.9.36).
| (a) | Find the time average power dissipation density in each region.
|
| (b) | What is the total time average power dissipated in
the sphere?
|
|
| 11.5.3* | Plane parallel perfectly conducting plates having the spacing d
are shorted by a perfectly conducting sheet in the plane x = 0, as
shown
in Fig. P11.5.3. A sheet having thickness 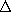 and conductivity and conductivity
 is in the plane x = -b and makes contact with the perfectly
conducting plates above and below. At their left edges, in the plane
x = -(a + b), a source of surface current density, K(t), is
connected to the plates. The regions to left and right of the
resistive sheet are free space, and w is large compared to a, b, and
d. is in the plane x = -b and makes contact with the perfectly
conducting plates above and below. At their left edges, in the plane
x = -(a + b), a source of surface current density, K(t), is
connected to the plates. The regions to left and right of the
resistive sheet are free space, and w is large compared to a, b, and
d.
 Figure P11.5.3
Figure P11.5.3
| (a) | Show that the total power dissipation and magnetic energy stored as defined on the right in (11.1.1), are

|
| (b) | Show that the integral on the left in (11.1.1) over the
surface
indicated by the dashed line in the figure gives the same result as
found in part (a).
|
|
| 11.5.4 | In Example 10.4.1, the applied field is Ho (t) = Hm cos (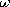 t) and sinsuoidal steady state conditions prevail. Determine the
time average power dissipation in the conducting sheet.
t) and sinsuoidal steady state conditions prevail. Determine the
time average power dissipation in the conducting sheet.
 Figure P11.5.5
Figure P11.5.5
|
| 11.5.5* | The cross-section of an N-turn circular solenoid having radius a
is shown in Fig. P11.5.5. It surrounds a thin cylindrical shell of
square cross-section, with length b on a side. This shell has
thickness 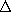 and conductivity and conductivity  , and is filled by a material
having permeability , and is filled by a material
having permeability  . Both the shell and the solenoid have a
length d perpendicular to the paper that is large compared to a. . Both the shell and the solenoid have a
length d perpendicular to the paper that is large compared to a.
| (a) | Given that the terminals of the solenoid are driven by the
current i1 = io cos 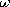 t and the sinusoidal steady state has been
established, integrate the time average power dissipation density over
the volume of the shell to show that the total time-average power
dissipation is t and the sinusoidal steady state has been
established, integrate the time average power dissipation density over
the volume of the shell to show that the total time-average power
dissipation is

|
| (b) | In the sinusoidal steady state, the time average Poynting
flux through a surface enclosing the shell goes into the time average
dissipation. Use this fact to obtain (a).
|
|
| 11.5.6 | In describing the response of macroscopic media to fields in the
sinusoidal steady state, it is convenient to use complex constitutive
laws. The complex permittivity is introduced by (19). Here
we introduce and illustrate the complex permeability. Suppose
that field quantities take the form

| (a) | Show that in a region where there is no macroscopic current density, the MQS laws require that



|
| (c) | Given that the spherical shell of Prob. 10.4.3 comprises each
element in the cubic array of Fig. P11.5.6, each sphere with spacing
s such that s  R, what is the complex permeability R, what is the complex permeability  defined such that
defined such that 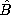 = = 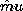 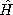 ? ?
|
| (d) | A macroscopic material composed of this
array of spheres is placed in the one-turn solenoid of rectangular
cross-section shown in Fig. P11.5.6. This configuration is long
enough in the z direction so that fringing fields can be ignored. At
their left edges, the perfectly conducting plates composing the top
and bottom of the solenoid are driven by a distributed current source,
K(t). With the fringing fields in the neighborhood of the left end
ignored, the resulting fields take the form H = Hz (x, t) iz
and E = Ey (x, t)iy. Use an
evaluation of the Poynting flux to determine the total time average
power dissipated in the length l, width d, and height a of the
material.
|
 Figure P11.5.6
Figure P11.5.6
|
| 11.5.7* | In the limit where the skin depth 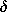 is small compared to the
length b, the magnetic field distribution in the conductor of Fig.
10.7.2 is given by (10.7.15). Show that (per unit y - z area) the
time average power dissipation associated with the current flowing in
the "skin" region is |Ks|2/2 is small compared to the
length b, the magnetic field distribution in the conductor of Fig.
10.7.2 is given by (10.7.15). Show that (per unit y - z area) the
time average power dissipation associated with the current flowing in
the "skin" region is |Ks|2/2 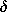 watts/m2. watts/m2.
|
| 11.5.8 | The conducting block shown in Fig. 10.7.2 has a length d in the z
direction.
|
| 11.5.9* | The toroid of Fig. 9.4.1 is filled with an insulating material
having the magnetization constitutive law of Prob. 9.4.3. Show that
from the terminals of the N1-turn coil, the circuit is equivalent
to one having an inductance L =  o N12 w2 /8R in
series with a resistance Rm = o N12 w2 /8R in
series with a resistance Rm =  o o  N12 w2/8R. N12 w2/8R.
|
| 11.5.10 | The toroid of Fig. 9.4.1 is filled by a material having the
magnetization characteristic shown in Fig. P11.5.10. A sinusoidal
current is supplied with a particular amplitude, i = (2Hc 2 R/N1) cos (
R/N1) cos (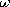 t). t).
 Figure P11.5.10
Figure P11.5.10
|
| | Electrical Forces on Macroscopic Media |
|---|
| 11.6.1* | A pair of perfectly conducting plates, the upper one fixed and
the lower one free to move with the horizontal displacement 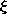 , have a
fixed spacing a as shown in Fig. P11.6.1. Show that the force of
electrical origin acting on the lower electrode in the , have a
fixed spacing a as shown in Fig. P11.6.1. Show that the force of
electrical origin acting on the lower electrode in the 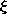 direction is
f = - direction is
f = -  o v2 d/2a. o v2 d/2a.
 Figure P11.6.1
Figure P11.6.1
|
| 11.6.2 | In Example 4.6.3, the capacitance per unit length of the pair of
parallel circular cylindrical conductors shown in Fig. 4.6.6 was
found. Determine the force per unit length acting on the right
cylinder in the x direction.
|
| 11.6.3* | The electric transducer shown in cross-section by Fig. P11.6.3
has cylindrical symmetry about the center line. A coaxial pair of
perfectly conducting electrodes having length l are excited at the
left end by a voltage source v(t). A perfectly insulating dielectric
material having permittivity  is free to slide in and out of the
annular region between electrodes. is free to slide in and out of the
annular region between electrodes.
 Figure P11.6.3
Figure P11.6.3
|
| 11.6.4 | The electrometer movement shown in Fig. P11.6.4 consists of
concentric, perfectly conducting tubes, the inner one free to move in
the axial direction.
| (a) | Ignore the fringing field and determine the
force of electrical origin acting in the direction of 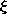 . .
|
| (b) | For
the energy conversion cycle of Demonstration 11.6.1, but for this
transducer, make dimensioned plots of the cycle in the (q, v) and
(f, 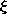 ) planes (analogous to those of Fig. 11.6.5). ) planes (analogous to those of Fig. 11.6.5).
|
| (c) | By
calculating both, show that the electrical energy input in one cycle
is equal to the work done on the external mechanical system.
|
 Figure P11.6.4
Figure P11.6.4
|
| 11.6.5* | Show that the vertical force on the nonlinear dielectric material
of Prob. 11.4.6 is

|
| | Macroscopic Magnetic Fields |
|---|
| 11.7.1* | Show that the force acting in the x direction on the movable
element of Prob. 9.7.5 (Note Prob. 11.4.4.) is

|
| 11.7.2 | Determine the force f(i, 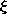 ) acting in the x direction on the
plunger of the magnetic circuit shown in Fig. P9.7.6. ) acting in the x direction on the
plunger of the magnetic circuit shown in Fig. P9.7.6.
 Figure P11.7.3
Figure P11.7.3
|
| 11.7.3* | The magnetic transducer shown in Fig. P11.7.3 consists of a
magnetic circuit in which the lower element is free to move in the x
and y directions. From the energy principle, ignoring fringing
fields, show that the force on this element is

|
| 11.7.4 | The magnetic circuit shown in cross-section by Fig. P11.7.4 has
cylindrical symmetry. A plunger of permeability  having outer
and inner radii a and b can suffer a displacement having outer
and inner radii a and b can suffer a displacement 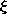 into the
annular gap of a magnetic circuit otherwise made of infinitely
permeable material. The coil has N turns. Assume that the left end
of the plunger is well within the magnetic circuit, so that fringing
fields can be ignored, and determine the force f(i, into the
annular gap of a magnetic circuit otherwise made of infinitely
permeable material. The coil has N turns. Assume that the left end
of the plunger is well within the magnetic circuit, so that fringing
fields can be ignored, and determine the force f(i, 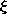 ) acting to
displace the plunger in the ) acting to
displace the plunger in the 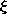 direction. direction.
 Figure P11.7.4
Figure P11.7.4
|
| 11.7.5* | The "variable reluctance" motor shown in cross-section in Fig.
P11.7.5 consists of an infinitely permeable yoke and an infinitely
permeable rotor element forming a magnetic circuit with two air gaps
of length 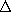 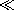 R. The system has depth d R. The system has depth d  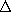 into
the paper. Assume that 0 < into
the paper. Assume that 0 < 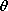 < <  , as shown, and show that
the torque caused by passing a current i through the two N-turn
coils is , as shown, and show that
the torque caused by passing a current i through the two N-turn
coils is  = - = -  o Rd N2 i2/ o Rd N2 i2/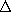 . .
 Figure P11.7.5
Figure P11.7.5
|
| 11.7.6 | A "two-phase" synchronous machine is constructed having a
cross-section like that shown in Fig. 11.7.7, except that there is an
additional winding on the stator. This is identical to the one shown
except that it is rotated 90 degrees in the clockwise direction. The
current in the stator winding shown in Fig. 11.7.7 is denoted by
ia, while that in the additional winding is ib. Thus, the
magnetic axes of ia and ib, respectively, are upward and to the
right. With Ls, Lr, and M given constants, the inductance
matrix is

| (a) | Determine the coenergy wm' (ia, ib, 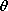 ). ).
|
| (b) | Find the torque on the rotor,  (ia, ib, (ia, ib, 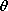 ). ).
|
| (c) | With ia = I cos (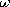 t) and ib = I sin ( t) and ib = I sin (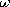 t), where I and
t), where I and 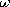 are given constants, argue that the
magnetic axis produced by the stator rotates with the angular
velocity are given constants, argue that the
magnetic axis produced by the stator rotates with the angular
velocity 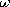 . .
|
| (d) | Using these current constraints together with ir = Ir
and 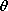 = = 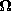 t - t -  , where Ir, , where Ir,  and and 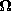 are constants, show that under synchronous conditions (where
are constants, show that under synchronous conditions (where 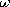 = =
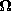 ), the torque is ), the torque is  = MI Ir sin ( = MI Ir sin ( ). ).
|
|
| | Forces on Microscopic Electric and Magnetic Dipoles |
|---|
| 11.8.1* | In a uniform electric field E, a perfectly conducting
particle having radius R has a dipole moment p = 4  o R3
E. Provided that R is short compared to
distances over which the field varies, this gives a good approximation
to p, even where the field is not uniform. Such a particle is
shown at the location x = X, y = Y in Fig. P11.8.1, where it is
subject to the field produced by a periodic potential o R3
E. Provided that R is short compared to
distances over which the field varies, this gives a good approximation
to p, even where the field is not uniform. Such a particle is
shown at the location x = X, y = Y in Fig. P11.8.1, where it is
subject to the field produced by a periodic potential 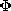 = Vo cos
( = Vo cos
( x) imposed in the plane y = 0. x) imposed in the plane y = 0.
| (a) | Show that the potential imposed in the region 0 < y is Vo cos ( x) exp (- x) exp (- y). y).
|
| (b) | Show that, provided that the particle has no net charge,
the force on the particle is

|
 Figure P11.8.1
Figure P11.8.1
|
| 11.8.2 | The perfectly conducting particle described in Prob. 11.8.1,
carrying no net charge but polarized by the imposed electric field, is
subjected to the field of a charge Q located at the origin of a
spherical coordinate system. In terms of its location R relative to
the charged particle at the origin, determine the force on the
particle.
 Figure P11.8.3
Figure P11.8.3
|
| 11.8.3* | In Fig. P11.8.3, permanent magnets in the lower half-space are
represented by the magnetization density M = Mo cos ( x)iy, where Mo and
x)iy, where Mo and  are given positive constants. are given positive constants.
|
| 11.8.4 | A small "infinitely permeable" particle of radius R is a distance
Z above an infinitely permeable plane, as shown in Fig. P11.8.4. A
uniform field H = Ho iz is imposed. Assume that R 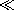 Z,
and use (27) to approximate the dipole moment induced
in the particle. The effect of the infinitely permeable plane on the
field induced by this dipole is equivalent to that of a second image
dipole located at z = -Z. Thus, there is a force of attraction between
the magnetized particle and the infinite plane that is equivalent to
that attracting the dipole to its image. Determine the force in the z
direction on the particle. Z,
and use (27) to approximate the dipole moment induced
in the particle. The effect of the infinitely permeable plane on the
field induced by this dipole is equivalent to that of a second image
dipole located at z = -Z. Thus, there is a force of attraction between
the magnetized particle and the infinite plane that is equivalent to
that attracting the dipole to its image. Determine the force in the z
direction on the particle.
 Figure P11.8.4
Figure P11.8.4
|
| | Macroscopic Force Densities |
|---|
| 11.9.1 | In Prob. 11.7.2, the total force on a magnetizable plunger is
found (Fig. P9.7.6). Find this same force by integrating the force
density, (14), over the volume of the plunger.
|
| 11.9.2* | In Example 10.3.1, the transient current induced by applying a
magnetic field intensity Ho to a conducting shell is determined.
| (a) | Show that there is a radial magnetic force per unit area
acting on the shell Tr =  o K(Ho + Hi)/2. (Note that the
thin-shell model implies that H varies in an essentially linear
fashion with R inside the shell.) o K(Ho + Hi)/2. (Note that the
thin-shell model implies that H varies in an essentially linear
fashion with R inside the shell.)
|
| (b) | Specifically, show that

|
|
| 11.9.3 | In Example 10.4.1, the transient current induced in a conducting
shell by the application of a transverse magnetic field is found.
Suppose that the magnetizable core is absent.
|


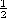 C vc2 +
C vc2 + 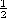 Li2.
Argue that w
is the energy stored in the inductor and capacitor, while i2 R is
the power dissipated in the resistor.
Li2.
Argue that w
is the energy stored in the inductor and capacitor, while i2 R is
the power dissipated in the resistor. in the annulus b < r <
a, as shown in Fig. P11.3.2. The length l is large compared to
a. A voltage source v drives the system at the left, while the
electrodes are "open" at the right. Assume that v(t) is so slowly
varying that the voltage can be regarded as independent of z.
in the annulus b < r <
a, as shown in Fig. P11.3.2. The length l is large compared to
a. A voltage source v drives the system at the left, while the
electrodes are "open" at the right. Assume that v(t) is so slowly
varying that the voltage can be regarded as independent of z.

 and uniform permittivity
and uniform permittivity
 , while the surrounding region, where b < r < a, is free space. A
distributed voltage source v(t) constrains the potential difference
between the outer edges of the electrodes. Assume that the system is EQS.
, while the surrounding region, where b < r < a, is free space. A
distributed voltage source v(t) constrains the potential difference
between the outer edges of the electrodes. Assume that the system is EQS.
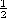 Li2 to show that L is as given by
(8.5.20).
Li2 to show that L is as given by
(8.5.20).
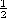 L i2 to find L.
L i2 to find L.

 a =
a =  o and
the region where B =
o and
the region where B =  b H now
filled with a material having the constitutive law
b H now
filled with a material having the constitutive law

 exp (j
exp (j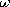 t)]. The sinusoidal steady state has been
established. Show that the time average power dissipation in the
lossy dielectrics is
t)]. The sinusoidal steady state has been
established. Show that the time average power dissipation in the
lossy dielectrics is

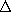 and conductivity
and conductivity
 is in the plane x = -b and makes contact with the perfectly
conducting plates above and below. At their left edges, in the plane
x = -(a + b), a source of surface current density, K(t), is
connected to the plates. The regions to left and right of the
resistive sheet are free space, and w is large compared to a, b, and
d.
is in the plane x = -b and makes contact with the perfectly
conducting plates above and below. At their left edges, in the plane
x = -(a + b), a source of surface current density, K(t), is
connected to the plates. The regions to left and right of the
resistive sheet are free space, and w is large compared to a, b, and
d.

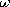 t) and sinsuoidal steady state conditions prevail. Determine the
time average power dissipation in the conducting sheet.
t) and sinsuoidal steady state conditions prevail. Determine the
time average power dissipation in the conducting sheet.

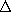 and conductivity
and conductivity  , and is filled by a material
having permeability
, and is filled by a material
having permeability  . Both the shell and the solenoid have a
length d perpendicular to the paper that is large compared to a.
. Both the shell and the solenoid have a
length d perpendicular to the paper that is large compared to a.


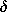 is small compared to the
length b, the magnetic field distribution in the conductor of Fig.
10.7.2 is given by (10.7.15). Show that (per unit y - z area) the
time average power dissipation associated with the current flowing in
the "skin" region is |Ks|2/2
is small compared to the
length b, the magnetic field distribution in the conductor of Fig.
10.7.2 is given by (10.7.15). Show that (per unit y - z area) the
time average power dissipation associated with the current flowing in
the "skin" region is |Ks|2/2
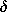 watts/m2.
watts/m2.
 o N12 w2 /8R in
series with a resistance Rm =
o N12 w2 /8R in
series with a resistance Rm =  o
o  N12 w2/8R.
N12 w2/8R.
 R/N1) cos (
R/N1) cos (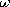 t).
t).

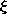 , have a
fixed spacing a as shown in Fig. P11.6.1. Show that the force of
electrical origin acting on the lower electrode in the
, have a
fixed spacing a as shown in Fig. P11.6.1. Show that the force of
electrical origin acting on the lower electrode in the 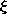 direction is
f = -
direction is
f = -  o v2 d/2a.
o v2 d/2a.

 is free to slide in and out of the
annular region between electrodes.
is free to slide in and out of the
annular region between electrodes.




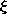 ) acting in the x direction on the
plunger of the magnetic circuit shown in Fig. P9.7.6.
) acting in the x direction on the
plunger of the magnetic circuit shown in Fig. P9.7.6.


 having outer
and inner radii a and b can suffer a displacement
having outer
and inner radii a and b can suffer a displacement 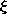 into the
annular gap of a magnetic circuit otherwise made of infinitely
permeable material. The coil has N turns. Assume that the left end
of the plunger is well within the magnetic circuit, so that fringing
fields can be ignored, and determine the force f(i,
into the
annular gap of a magnetic circuit otherwise made of infinitely
permeable material. The coil has N turns. Assume that the left end
of the plunger is well within the magnetic circuit, so that fringing
fields can be ignored, and determine the force f(i, 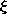 ) acting to
displace the plunger in the
) acting to
displace the plunger in the 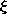 direction.
direction.

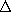
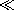 R. The system has depth d
R. The system has depth d 
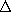 into
the paper. Assume that 0 <
into
the paper. Assume that 0 < 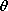 <
<  , as shown, and show that
the torque caused by passing a current i through the two N-turn
coils is
, as shown, and show that
the torque caused by passing a current i through the two N-turn
coils is  = -
= -  o Rd N2 i2/
o Rd N2 i2/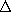 .
.



 o R3
E. Provided that R is short compared to
distances over which the field varies, this gives a good approximation
to p, even where the field is not uniform. Such a particle is
shown at the location x = X, y = Y in Fig. P11.8.1, where it is
subject to the field produced by a periodic potential
o R3
E. Provided that R is short compared to
distances over which the field varies, this gives a good approximation
to p, even where the field is not uniform. Such a particle is
shown at the location x = X, y = Y in Fig. P11.8.1, where it is
subject to the field produced by a periodic potential 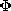 = Vo cos
(
= Vo cos
( x) imposed in the plane y = 0.
x) imposed in the plane y = 0.


 x)iy, where Mo and
x)iy, where Mo and  are given positive constants.
are given positive constants.
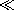 Z,
and use (27) to approximate the dipole moment induced
in the particle. The effect of the infinitely permeable plane on the
field induced by this dipole is equivalent to that of a second image
dipole located at z = -Z. Thus, there is a force of attraction between
the magnetized particle and the infinite plane that is equivalent to
that attracting the dipole to its image. Determine the force in the z
direction on the particle.
Z,
and use (27) to approximate the dipole moment induced
in the particle. The effect of the infinitely permeable plane on the
field induced by this dipole is equivalent to that of a second image
dipole located at z = -Z. Thus, there is a force of attraction between
the magnetized particle and the infinite plane that is equivalent to
that attracting the dipole to its image. Determine the force in the z
direction on the particle.


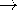 0 and
show that the one-dimensional form of (3) results.
0 and
show that the one-dimensional form of (3) results.





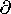 W/
W/




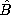 =
= 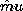
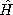 ?
?

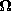 t -
t - 


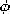 o + H
o + H