| 12.1.1*
| In Sec. 10.1, the electric field in an MQS system was divided
into a particular part Ep satisfying Faraday's law, and an
irrotational part Eh. The latter was adjusted to make the sum
satisfy appropriate boundary conditions. Show that in terms of 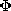 and A, as defined in this section, Ep = -
and A, as defined in this section, Ep = -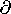 A/ A/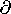 t
and Eh = - t
and Eh = -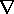 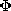 , where these potentials satisfy (12.1.8)
and (12.1.10) with the time derivatives neglected. , where these potentials satisfy (12.1.8)
and (12.1.10) with the time derivatives neglected.
|
| 12.1.2 | In Sec. 3.3, dimensional arguments were used to show that the
quasistatic limits were valid in a system having a typical length L
and time  if L/c if L/c 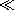  . Use similar arguments to show that
the second term on the right in either (12.1.8) or (12.1.10) is
negligible when this condition prevails. Note that the resulting
equations are those for MQS (8.1.5) and EQS (4.2.2) systems. . Use similar arguments to show that
the second term on the right in either (12.1.8) or (12.1.10) is
negligible when this condition prevails. Note that the resulting
equations are those for MQS (8.1.5) and EQS (4.2.2) systems.
|
| | Electrodynamic Fields of Source Singularities |
|---|
| 12.2.1 | An electric dipole has q(t) = 0 for t < 0 and t > T. When 0 <
t < T, q(t) = Q[1 - cos (2 t/T)]/2. Use sketches similar to
those of Figs. 12.2.5 and 12.2.6 to show the field distributions when
t < T and T < t. t/T)]/2. Use sketches similar to
those of Figs. 12.2.5 and 12.2.6 to show the field distributions when
t < T and T < t.
|
| 12.2.2* | Use the "interchange of variables" property of Maxwell's
equations to show that the sinusoidal steady state far fields of a
magnetic dipole, (12.2.35) and (12.2.36), follow directly from (12.2.23),
(12.2.24), and (12.2.32).
|
| 12.2.3* | A magnetic dipole has a moment m(t) having the time dependence
shown in Fig. 12.2.5a where dq(t) 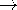 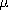 m(t). Show
that the fields are then much as shown in Fig. 12.2.6 with E m(t). Show
that the fields are then much as shown in Fig. 12.2.6 with E
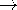 H, H H, H 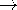 -E, and -E, and 
 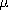 . .
|
| | Antenna Radiation Fields in the Sinusoidal Steady State |
|---|
| 12.4.1 | An "end-fed" antenna consists of a wire stretching between z = 0,
where it is driven by the current Io cos ( t - t -
 o), and z = l. At z = l, it is terminated in such a
resistance that the current distribution over its length is a wave
traveling with the velocity of light in the z direction; i(z, t) =
Re [Io exp [j( o), and z = l. At z = l, it is terminated in such a
resistance that the current distribution over its length is a wave
traveling with the velocity of light in the z direction; i(z, t) =
Re [Io exp [j( t - kz + t - kz +  o)]] where k o)]] where k 
 /c. /c.
|
| 12.4.2* | An antenna is modeled by a distribution of incremental magnetic
dipoles, as shown in Fig. P12.4.2. Define  (z) as a dipole moment
per unit length so that for an incremental dipole located at z' , (z) as a dipole moment
per unit length so that for an incremental dipole located at z' ,
 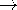  (z' )dz'. Given (z' )dz'. Given  , show that , show that
 where
where

 Figure P12.4.2
Figure P12.4.2
|
| 12.4.3 | A linear distribution of magnetic dipoles, described in general
in Prob. 12.4.2, is excited so that  (z' ) = - (z' ) = -  o exp (j o exp (j o) sin o) sin 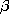 (z - l)/sin (z - l)/sin 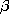 l, 0 l, 0  z z
 l where l where 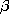 is a given parameter (not necessarily is a given parameter (not necessarily  /c). Determine
/c). Determine 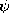 o( o(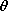 ). ).
|
| 12.4.4* | For the three-element array shown in Fig. P12.4.4, the spacing is
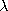 /4. /4.

| (a) | Show that the array factor is
|
| (b) | Show that for an array of in-phase short dipoles, the
"broadside" radiation intensity pattern is

|
| (c) | Show that for an array of short dipoles differing
progressively by 90 degrees so that  1 - 1 -  o = o =  /2 and /2 and
 2 - 2 -  o = o =  , the end-fire radiation pattern is , the end-fire radiation pattern is

|
 Figure P12.4.4
Figure P12.4.4
|
| 12.4.5 | Collinear elements have the half-wave spacing and configuration
shown in Fig. P12.5.5.
 Figure P12.5.5
Figure P12.5.5
|
| | Complex Poynting's Theorem and Radiation Resistance |
|---|
| 12.5.1* | A center-fed wire antenna has a length of 3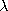 /2. Show that
its radiation resistance in free space is 104 /2. Show that
its radiation resistance in free space is 104 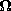 . (The definite
integral can be evaluated numerically.) . (The definite
integral can be evaluated numerically.)
|
| 12.5.2 | The spherical coil of Example 8.5.1 is used as a magnetic dipole
antenna. Its diameter is much less than a wavelength, and its
equivalent circuit is an inductance L in parallel with a radiation
resistance Rrad. In terms of the radius R, number of
turns N, and frequency  , what are L and Rrad? , what are L and Rrad?
|
| | Waves
|
|---|
| 12.6.1* | In the plane y = 0, Kz = 0 and the surface charge density is
given as the traveling wave  s = Re s = Re  o exp
[j( o exp
[j( t - kx x)] = Re [ t - kx x)] = Re [ o exp (-jkx x) exp
(j o exp (-jkx x) exp
(j t)], where t)], where  o, o,  , and kx are given real
numbers. , and kx are given real
numbers.

|
| 12.6.2 | In the plane y = 0, the surface current density is a standing wave,
K = Re [iz Ko sin (kx x) exp (j t)], and
there is no surface charge density. t)], and
there is no surface charge density.
|
| 12.6.3* | In the planes y =  d/2, shown in Fig. P12.6.3, there are
surface current densities Kz = Re d/2, shown in Fig. P12.6.3, there are
surface current densities Kz = Re  exp [j( exp [j( t
- kx x)], where t
- kx x)], where  = =  a at y = d/2 and a at y = d/2 and  = =  b at y = -d/2. The surface charge density is zero in each plane. b at y = -d/2. The surface charge density is zero in each plane.
|
| 12.6.4 | Surface charges in the planes y =  d/2 shown in Fig. P12.7.3
have the densities d/2 shown in Fig. P12.7.3
have the densities  s = Re s = Re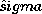 exp [j( exp [j( t - kx x)] where
t - kx x)] where 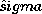 = = 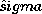 a at y = d/2 and a at y = d/2 and
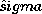 = = 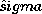 b at y = -d/2. b at y = -d/2.
related to produce field cancellation in region (b)?
| (a) | How should 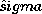 a and a and 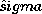 b be b be
|
| (b) | Under this condition, what is Hz in region (a)?
|
| (c) | What frequencies give a maximum Hz in region (a),
and what is the direction of propagation under this condition?
|
 Figure P12.7.3
Figure P12.7.3
|
| | Conductors
|
|---|
| 12.7.1* | An antenna consists of a ground plane with a 3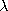 /4 vertical
element in which a "quarter-wave stub" is used to make the current
in the top half-wavelength in phase with that in the bottom
quarter-wavelength. In each section, the current has the sinusoidal
distribution shown in Fig. P12.7.1. Show that the radiation
intensity factor is /4 vertical
element in which a "quarter-wave stub" is used to make the current
in the top half-wavelength in phase with that in the bottom
quarter-wavelength. In each section, the current has the sinusoidal
distribution shown in Fig. P12.7.1. Show that the radiation
intensity factor is

 Figure P12.7.1
Figure P12.7.1
 Figure P12.7.2
Figure P12.7.2
|
| 12.7.2 | A vertical half-wave antenna with a horizontal perfectly
conducting ground plane is shown in Fig. P12.7.2. What is its
radiation resistance?
|
| 12.7.3 | Plane parallel perfectly conducting plates in the planes x =  a/2 form the walls of a waveguide, as shown in Fig. 12.7.3.
Waves in the free-space region between are excited by a sheet of
surface charge density
a/2 form the walls of a waveguide, as shown in Fig. 12.7.3.
Waves in the free-space region between are excited by a sheet of
surface charge density  s = Re s = Re  o cos ( o cos ( x/a)
exp (j x/a)
exp (j t) and Kz = 0. t) and Kz = 0.
solutions that meet both the continuity conditions at the sheet and
the boundary conditions on the perfectly conducting plates.) Are
they TE or TM?

|
| 12.7.4 | Consider the configuration of Prob. 12.7.3, but with  s = 0
and Kz = Re s = 0
and Kz = Re  o cos ( o cos ( x/a) exp (j x/a) exp (j t) in the plane y = 0. Complete parts (a)-(d) of Prob. 12.7.3.
t) in the plane y = 0. Complete parts (a)-(d) of Prob. 12.7.3.
|


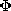 and A, as defined in this section, Ep = -
and A, as defined in this section, Ep = -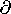 A/
A/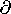 t
and Eh = -
t
and Eh = -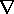
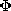 , where these potentials satisfy (12.1.8)
and (12.1.10) with the time derivatives neglected.
, where these potentials satisfy (12.1.8)
and (12.1.10) with the time derivatives neglected.
 if L/c
if L/c 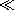
 . Use similar arguments to show that
the second term on the right in either (12.1.8) or (12.1.10) is
negligible when this condition prevails. Note that the resulting
equations are those for MQS (8.1.5) and EQS (4.2.2) systems.
. Use similar arguments to show that
the second term on the right in either (12.1.8) or (12.1.10) is
negligible when this condition prevails. Note that the resulting
equations are those for MQS (8.1.5) and EQS (4.2.2) systems.
 t/T)]/2. Use sketches similar to
those of Figs. 12.2.5 and 12.2.6 to show the field distributions when
t < T and T < t.
t/T)]/2. Use sketches similar to
those of Figs. 12.2.5 and 12.2.6 to show the field distributions when
t < T and T < t.
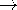
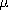 m(t). Show
that the fields are then much as shown in Fig. 12.2.6 with E
m(t). Show
that the fields are then much as shown in Fig. 12.2.6 with E
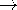 H, H
H, H 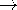 -E, and
-E, and 

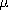 .
.
 t -
t -
 o), and z = l. At z = l, it is terminated in such a
resistance that the current distribution over its length is a wave
traveling with the velocity of light in the z direction; i(z, t) =
Re [Io exp [j(
o), and z = l. At z = l, it is terminated in such a
resistance that the current distribution over its length is a wave
traveling with the velocity of light in the z direction; i(z, t) =
Re [Io exp [j( t - kz +
t - kz +  o)]] where k
o)]] where k 
 /c.
/c.
 (z) as a dipole moment
per unit length so that for an incremental dipole located at z' ,
(z) as a dipole moment
per unit length so that for an incremental dipole located at z' ,

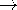
 (z' )dz'. Given
(z' )dz'. Given  , show that
, show that



 (z' ) = -
(z' ) = -  o exp (j
o exp (j o) sin
o) sin 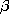 (z - l)/sin
(z - l)/sin 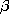 l, 0
l, 0  z
z
 l where
l where 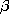 is a given parameter (not necessarily
is a given parameter (not necessarily  /c). Determine
/c). Determine 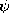 o(
o(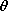 ).
).
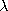 /4.
/4.



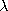 /2. Show that
its radiation resistance in free space is 104
/2. Show that
its radiation resistance in free space is 104 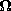 . (The definite
integral can be evaluated numerically.)
. (The definite
integral can be evaluated numerically.)
 , what are L and Rrad?
, what are L and Rrad?
 s = Re
s = Re  o exp
[j(
o exp
[j( t - kx x)] = Re [
t - kx x)] = Re [ o exp (-jkx x) exp
(j
o exp (-jkx x) exp
(j t)], where
t)], where  o,
o,  , and kx are given real
numbers.
, and kx are given real
numbers.

 t)], and
there is no surface charge density.
t)], and
there is no surface charge density.
 d/2, shown in Fig. P12.6.3, there are
surface current densities Kz = Re
d/2, shown in Fig. P12.6.3, there are
surface current densities Kz = Re  exp [j(
exp [j( t
- kx x)], where
t
- kx x)], where  =
=  a at y = d/2 and
a at y = d/2 and  =
=  b at y = -d/2. The surface charge density is zero in each plane.
b at y = -d/2. The surface charge density is zero in each plane.
 d/2 shown in Fig. P12.7.3
have the densities
d/2 shown in Fig. P12.7.3
have the densities  s = Re
s = Re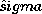 exp [j(
exp [j( t - kx x)] where
t - kx x)] where 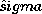 =
= 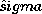 a at y = d/2 and
a at y = d/2 and
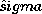 =
= 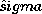 b at y = -d/2.
b at y = -d/2.

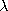 /4 vertical
element in which a "quarter-wave stub" is used to make the current
in the top half-wavelength in phase with that in the bottom
quarter-wavelength. In each section, the current has the sinusoidal
distribution shown in Fig. P12.7.1. Show that the radiation
intensity factor is
/4 vertical
element in which a "quarter-wave stub" is used to make the current
in the top half-wavelength in phase with that in the bottom
quarter-wavelength. In each section, the current has the sinusoidal
distribution shown in Fig. P12.7.1. Show that the radiation
intensity factor is



 a/2 form the walls of a waveguide, as shown in Fig. 12.7.3.
Waves in the free-space region between are excited by a sheet of
surface charge density
a/2 form the walls of a waveguide, as shown in Fig. 12.7.3.
Waves in the free-space region between are excited by a sheet of
surface charge density  s = Re
s = Re  o cos (
o cos ( x/a)
exp (j
x/a)
exp (j t) and Kz = 0.
t) and Kz = 0.

 s = 0
and Kz = Re
s = 0
and Kz = Re  o cos (
o cos ( x/a) exp (j
x/a) exp (j t) in the plane y = 0. Complete parts (a)-(d) of Prob. 12.7.3.
t) in the plane y = 0. Complete parts (a)-(d) of Prob. 12.7.3.
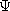 (
(






 .
.