The theme in this chapter has been the transmission line. It has been used to represent the evolution of electromagnetic fields through structures generally comprised of a pair of "conductors" embedded in a less conducting, and often highly insulating, medium. We have confined ourselves to systems that are uniform in the direction of evolution, the z direction.
If the conductors can be regarded as perfectly conducting, and the
medium in which they are embedded as having uniform permeability,
permittivity, and conductivity, the fields are exactly TEM, regardless
of the cross-sectional geometry. The relevant laws and distributed
parameter model are summarized in Table 14.10.1. Identification of
variables as illustrated in the table make the transmission line
exactly equivalent to a plane wave. Whether L, C, or G
represent fields propagating along the conductors or a plane wave,
LC = 
 and C/G =
and C/G =  /
/ .
.
TABLE 14.10.1 TRANSMISSION LINE EQUIVALENTS
|
|
(14.8.4) (14.8.5) |
 |
 `
`  |
 |
Much of this chapter is devoted to describing the limit where the
conductors are not only perfect, but the medium has negligible
conductivity (G = 0). Transients on this "ideal" transmission
line are described by using the relations summarized in Table
14.10.2. The voltage and current at any position and time (z, t)
are superpositions of wave components that propagate with the velocity
c. These forward and backward wave components are, respectively,
invariant on lines in the z - t plane of constant  and
and
 . Along those lines originating on initial conditions, the
wave components are as summarized in the second row of the table.
The last two rows summarize how the reflected wave component is
determined from the incident component at two common terminations.
. Along those lines originating on initial conditions, the
wave components are as summarized in the second row of the table.
The last two rows summarize how the reflected wave component is
determined from the incident component at two common terminations.
TABLE 14.10.2 WAVE TRANSIENTS
|
|
(14.3.9) (14.3.10) (14.3.11) (14.3.12) (14.3.1) |
 |
|
|
(14.3.18) (14.3.19) |
 |
 |
(14.4.8)
|
 |
 |
(14.4.10) |  |
A summary of the relations used to describe the ideal line in the
sinusoidal steady state is given in Table 14.10.3. Because it has a
magnitude that is constant and a phase that increases linearly with
z, the evolution of voltage and current and of their ratio, the
impedance Z(z), is conveniently pictured in terms of the complex
reflection coefficient,  (z). Relations and the complex
(z). Relations and the complex
 plane are illustrated in the first row. The mappings of the
impedance and of the admittance onto this plane, respectively, are
summarized by the second and third rows. Because the magnitude of
plane are illustrated in the first row. The mappings of the
impedance and of the admittance onto this plane, respectively, are
summarized by the second and third rows. Because the magnitude of
 is constant over a uniform length of line, the trajectory of
Z(z) or Y(z) is on a circle of constant radius in the directions
of the generator or the load, as indicated. These Smith charts give
a convenient overview of how the impedance and admittance vary with
position.
is constant over a uniform length of line, the trajectory of
Z(z) or Y(z) is on a circle of constant radius in the directions
of the generator or the load, as indicated. These Smith charts give
a convenient overview of how the impedance and admittance vary with
position.
TABLE 14.10.3 SINUSOIDAL-STEADY STATE (R=0, G=0)
|
B = w |
(14.5.5)
(14.5.6)
(14.6.2) (14.3.12) (14.5.5) |
 |
|
|
(14.6.1) (14.6.3) |
 |
| (14.6.12) |  |
In Sec. 14.7, a shunt conductance per unit length, G, (to represent losses in the material between the transmission line conductors) and a series resistance per unit length, R, (for losses in the conductors themselves) was added to the distributed parameter transmission line representation. For the limiting case where the conductors were infinitely conducting, R = 0, and the material between of uniform properties, the fields represented by the line were exactly TEM. In the case where the material properties did vary over the cross section, the distributed parameter picture provided a useful model for the line provided that the wavelength was long compared to the cross-sectional dimensions. In specific terms, this model gave the opportunity to consider the dynamical processes considered in Chaps. 7, 10, and 12 (charge relaxation, magnetic diffusion and electromagnetic wave propagation, respectively) in one self consistent situation. What was learned will be generalized in the review of the processes given in Secs. 15.3-15.4.
In Sec. 14.9, where G = 0 but R was finite, the specific objective was to understand how the transmission line concept could be used to approximate conductor losses. A broader objective was to again illustrate the use of the distributed parameter line as a model, representing the fields at frequencies sufficiently low so that the wavelength is long compared with the transverse dimensions.


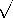 LC
LC