Transmission lines are generally connected to a source and to a load, as shown in Fig. 14.4.1a. More complex systems composed of interconnected transmission lines can usually be decomposed into subsystems having this basic configuration. A generator at z = 0 is connected to a load at z = l by a transmission line having the length l. In this section, we build upon the traveling wave picture introduced in Sec. 14.3 to describe transients at a boundary initiated by a source.
Fig 14.4.1 (a)Transmission line with terminations. (b) Initial and boundary conditions in z - t plane. In picturing the evolution with time of the voltage V(z, t) and current I(z, t) on a terminated line, it is again helpful to use the z - t plane shown in Fig. 14.4.1b. The load and generator impose boundary conditions at z = l and z = 0. In addition to satisfying these conditions, the distributions of V and I must also satisfy the respective initial values V = Vi(z) and I = Ii(z) when t = 0, introduced in Sec. 14.3. Thus, our goal is to find V and I in the
-shaped region of z - t space shown in Fig. 14.4.1b.
In Sec. 14.3, we found that the transmission line equations, (14.1.4) and (14.1.5), have solutions
where
and c =
and Zo =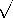
(L/C).
A mathematical way of saying that V+ and V-, respectively, represent waves traveling in the +z and -z directions is to say that these quantities are invariants on the characteristic lines
= constant and
= constant in the z - t plane.
There are two steps in finding V and I.
- First, the initial conditions, and now the boundary conditions as well, are used to determine V+ and V- along the two families of characteristic lines in the region of the z - t plane of interest. This is done with the understanding that causality prevails in the sense that the dynamics evolve in the "direction" of increasing time. Thus it is where a characteristic line enters the
- Second, the solution at a given point of intersection for the lines
To complete the first step, note that a characteristic line passing through a given point P has three possible origins. First, it can originate on the t = 0 axis, in which case the invariants, V
, are determined by the initial conditions. This was the only possibility on the infinite transmission line considered in Sec. 14.3. The initial voltage and current where the characteristic line originates when t = 0 in Fig. 14.4.2 is used to evaluate (1) and (2), and the simultaneous solution of these expressions then gives the desired invariants.
Fig 14.4.2 Characteristic lines originating on initial conditions. The second origin of a characteristic line is the boundary at z = l, as shown in Fig. 14.4.3. In particular, we consider the load resistance RL as the termination that imposes the boundary condition
Fig 14.4.3 Characteristic line originating on load. The problems will illustrate how the same approach illustrated here can also be used to describe terminations composed of arbitrary circuits. Certainly, the case where the load is a pure resistance is the most important type of termination, for reasons that will be clear shortly.
Again, because phenomena proceed in the +t "direction," the incident wave V+ and the boundary condition at z = l conspire to determine the reflected wave V- on the characteristic line
and solve for V-.
Here, V+ and V- are evaluated at z = l, and hence with
L and determine V-.
The third possible origin of a characteristic line passing through the given point P is on the boundary at z = 0, as shown in Fig. 14.4.4. Here the line has been terminated in a source modeled as an ideal voltage source, Vg(t), in series with a resistance Rg. In this case, it is the wave traveling in the -z direction (represented by V- and incident on the boundary from the left in Fig. 14.4.4) that combines with the boundary condition there to determine the reflected wave V+.
Fig 14.4.4 Characteristic lines originating on generator end of line. The boundary condition is the constraint of the circuit on the voltage and current at the terminals.
Substitution of (1) and (2) then gives an expression that can be solved for V+, given V- and Vg(t).
The following examples illustrate the two steps necessary to determine the transient response. First, V
Matching
The reflection of waves from the terminations of a line results in responses that can persist long after a signal has propagated the length of the transmission line. As a practical matter, it is therefore often desirable to eliminate reflections by matching the line.
From (8), it follows that wave reflection is eliminated at the load by making the load resistance equal to the characteristic impedance of the line, RL = Zo. Similarly, from (10), there will be no reflection of the wave V- at the source if the resistance Rg is made equal to Zo.
Consider first an example in which the response is made simple because the line is matched to its load.
Example 14.4.1. Matching
In the configuration shown in Fig. 14.4.5a, the load has a resistance RL while the generator is an ideal voltage source Vg(t) in series with the resistor Rg. The load is matched to the line, RL = Zo. As a result, according to (8), there are no V- waves on characteristics originating at the load.
Fig 14.4.5 (a) Matched line. (b) Wave components in z - t plane. (c) Response in z - t plane. Suppose that the driving voltage consists of a pulse of amplitude Vp and duration T, as shown in Fig. 14.4.5b. Further, suppose that when t = 0 the line voltage and current are both zero, Vi = 0, and Ii = 0. Then, it follows from (4) and (5) that V+ and V- are both zero on the respective characteristic lines originating on the t = 0 axis, as shown in Fig. 14.4.5b. By design, (8) gives V- = 0 for the
It follows from (1) and (2) that V and I are as shown in Fig. 14.4.5. Because V- = 0, the voltage and current both take the form of a pulse of temporal duration T and spatial length cT, propagating from source to load with the velocity c.
To express analytically what has been found, we know that at z = 0, V- = 0 and in turn from (10) that at z = 0,
This is the value of V+ along any line of constant
We can express this result in terms of z - t by introducing
Regardless of the shape of the voltage pulse, it appears undistorted at some location z but delayed by z/c.
Note that at any location on the matched line, including the terminals of the generator, V/I = Zo. The matched line appears to the generator as a resistance equal to the characteristic impedance of the line.
We have assumed in this example that the initial voltage and current are zero over the length of the line. If there were finite initial conditions, their response with the generator voltage set equal to zero would add to that obtained here because the wave equation is linear and superposition holds. Initial conditions give rise to waves V+ and V- propagating in the +z and -z directions, respectively. However, because there are no reflected waves at the load, the effect of the initial conditions could not last longer at the generator than the time l/c required for V- to reach z = 0 from z = l. They would not last longer at the load than the time 2l/c, when any resulting wave reflected from the generator would return to the load.
Open circuit and short circuit terminations result in complete reflection. For the open circuit, I = 0 at the termination, and it follows from (2) that V+ = V-. For a short, V = 0, and (1) requires that V+ = -V-. Note that these limiting relations follow from (8) by making RL infinite and zero in the respective cases.
In the following example, we see that an open circuit termination can result in a voltage that is momentarily as much as twice that of the generator.
Example 14.4.2. Open Circuit Termination
The transmission line of Fig. 14.4.6 is terminated in an infinite load resistance and driven by a generator modeled as a voltage source in series with a resistance Rg equal to the characteristic impedance Zo. As in the previous example, the driving voltage is a pulse of time duration T, as shown in Fig. 14.4.6b. When t = 0, V and I are zero. In this example, we illustrate the effect of matching the generator resistance to the line and of having complete reflection at the load.
Fig 14.4.6 (a) Open line. (b) Wave components in z - t plane. (c) Response in z - t plane. The boundary at z = l, (8), requires that
while that at the generator, (10), is simply
Because the generator is matched, this latter condition establishes V+ on characteristic lines originating on the z = 0 axis without regard for V-. These are summarized along the t axis in Fig. 14.4.6b.
To establish the values of V- on characteristic lines originating at the load, we must know values of the incident V+. Because I and V are both initially zero, the incident V+ at the load is zero until t=l/c. From (15), V- is also zero. From t = l/c until t = l/c + T, the incident V+ = Vp/2 and V- on the characteristic lines originating at the open circuit during this time interval follows from (15) as Vp/2. Finally, for all greater times, the incident wave is zero at the load and so also is the reflected wave. The values of V
With the values of V
The configuration of Fig. 14.4.6 was regarded in the previous example as an "open circuit transmission line" driven by a voltage source in series with a resistor. If we had been given the same configuration in Chap. 7, we would have taken it to be a "capacitor" in series with the resistor and the voltage source. The next example puts the EQS approximation in perspective by showing how it represents the dynamics when the resistance Rg is large compared to Zo. A clue as to what happens when this ratio is large comes from writing it in the form
Here, Rg Cl is the charging time of the capacitor and l/c is the electromagnetic wave transit time. When this ratio is large, the time for the transient to complete itself is many wave transit times. Thus, as will now be seen, the exponential charging of the capacitor is made up of many small steps associated with the electromagnetic wave passing "to and fro" over the length of the line.
Example 14.4.3. Quasistatic Transient as the Limit of an Electrodynamic Transient
The transmission line shown to the left in Fig. 14.4.7 is open at z = l and driven at z = 0 by a step in voltage, Vg = Vp u-1(t). We are especially interested in the response with the series resistance, Rg, very large compared to Zo. For simplicity, we assume that the initial voltage and current are zero.
Fig 14.4.7 Wave components of open line to a step in voltage in series with a high resistance. The boundary condition imposed at the open termination, where z = l, is I = 0. From (2),
while at the source, (10) pertains with Vg = Vp a constant
5 Be careful to distinguish the constant Vg as defined in this example from the source voltage Vg(t) = Vp U-1(t).
with the reflection coefficient of the generator defined as
Starting with characteristic lines originating at t = 0, where the initial conditions determine that V+ and V- are zero, we can now use these boundary conditions to determine V- on lines originating at the load and V+ on lines originating at z = 0. These values are shown in Fig. 14.4.7. Thus, V
The voltage and current now follow from (1) and (2). In particular, consider the response at the generator terminals, where z = 0. In Fig. 14.4.7, the t axis has been divided into intervals of duration 2l/c, the first denoted by N = 1, the second by N = 2, etc. We have found that the wave components incident on and reflected from the z = 0 boundary in the N-th interval are
It follows from (2) that the current at z = 0 during this time interval is
In turn, this current can be used to evaluate the terminal voltage.
With Rg/Zo very large, it follows from (20) that
In this same limit, the term 1 + Zo/Rg in (24) is essentially unity. Thus, (24) becomes approximately
We suspect that in the limit where the round-trip transit time 2l/c is short compared to the charging time
= Rg Cl, this voltage becomes the step response of the series capacitor and resistor.
To see that this is indeed the case, we exploit the fact that
by writing (26) in the form
It follows that in the limit where Zo/Rg is small,
Remember that N represents the interval of time during which the expression is valid. If we take the time as being that when the interval begins, then
Substitution of this expression for 2(N - 1) into (30) and use of (17) then shows that in this high-resistance limit, the voltage does indeed take the exponential form for a charging capacitor, (27), with a charging time
Fig 14.4.8 Response of open circuit transmission line to step in voltage in series with a high resistance. The smooth curve is predicted by the EQS model. The following demonstration is typical of a variety of demonstrations that are easily carried out using a good oscilloscope and a stretch of transmission line.
\begindemo1Transmission Line Matching, Reflection, and Quasistatic Charging The apparatus shown in Fig. 14.4.9 is all that is required to demonstrate the phenomena described in the examples. In a typical experiment, a 10 m length of cable is used, in which case the wave transit time is about 0.05
s. Thus, to resolve the transient, the oscilloscope must have a frequency response that extends to 100 MHz.
Fig 14.4.9 Oscilloscope displays voltage at terminals of line under conditions of Examples 14.4.1-3. To achieve matching of the generator, as called for in Example 14.4.2, Rg = Zo. Typically, for a coaxial cable, this is 50
.
To see the charging transient of Example 14.4.3 with 10 round trip transit times in the capacitive charging time, it follows from (17) that we should make Rg/Zo = 20. Thus, for a coaxial cable having Zo = 50
