The quasistatic laws are obtained from Maxwell's equations by neglecting either the magnetic induction or the electric displacement current.
ELECTROQUASISTATIC MAGNETOQUASISTATIC
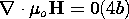The electromagnetic waves that result from the coupling of the magnetic induction and the displacement current are therefore neglected in either set of quasistatic laws. Before considering order of magnitude arguments in support of these approximate laws, we recognize their differing orders of importance.
In Chaps. 4 and 8 it will be shown that if the curl and divergence of a vector are specified, then that vector is determined.
In the EQS approximation, (1a) requires that E is essentially irrotational. It then follows from (3a) that if the charge density is given, both the curl and divergence of E are specified. Thus, Gauss' law and the EQS form of Faraday's law come first. In the MQS approximation, the displacement current is neglibible in (2b), while (4b) requires that H is solenoidal. Thus, if the current density is given, both the curl and divergence of H are known. Thsu, the MQS form of Ampère's law and the flux continuity conditiojn come first.
Implied by the approximate form of Ampère's law is the continuity condition of J, given by (5c).
In these relations, there are no time derivatives. This does not mean that the sources, and hence the fields, are not functions of time. But given the sources at a certain instant, the fields at that same instant are determined without regard for what the sources of fields were an instant earlier. Figuratively, a snapshot of the source distribution determines the field distribution at the same instant in time.
Generally, the sources of the fields are not known. Rather, because of the Lorentz force law, which acts to set charges into motion, they are determined by the fields themselves. It is for this reason that time rates of change come into play. We now bring in the equation retaining a time derivative.
Because H is often not crucial to the EQS motion of charges, it is eliminated from the picture by taking the divergence of (2a). Faraday's law makes it clear that a time varying H implies an induced electric field.
In the EQS approximation, H is usually a "leftover" quantity. In any case, once E and J are determined, H can be found by solving (2a) and (4a). In the MQS approximation, the charge density is a "leftover" quantity, which can be found by applying Gauss' law, (3b), to the previously determined electric field intensity.
In the EQS approximation, it is clear that with E and J determined from the "zero order" laws (5a)-(7a), the curl and divergence of H are known [(8a) and (9a)]. Thus, H can be found in an "after the fact" way. Perhaps not so obvious is the fact that in the MQS approximation, the divergence and curl of E are also determined without regard for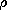
. The curl of E follows from Faraday's law, (7b), while the divergence is often specified by combining a conduction constitutive law with the continuity condition on J, (5b).
The differential quasistatic laws are summarized in Table 3.6.1 at the end of the chapter. Because there is a direct correspondence between terms in the differential and integral laws, the quasistatic integral laws are as summarized in Table 3.6.2. The conditions under which these quasistatic approximations are valid are examined in the next section.
