4.3
Superposition Principle

As illustrated in Cartesian coordinates by (4.2.3), Poisson's equation is a linear second-order differential equation relating the potential (r) to the charge distribution (r). By "linear" we mean that the coefficients of the derivatives in the differential equation are not functions of the dependent variable . An important consequence of the linearity of Poisson's equation is that (r) obeys the superposition principle. It is perhaps helpful to recognize the analogy to the superposition principle obeyed by solutions of the linear ordinary differential equations of circuit theory. Here the principle can be shown as follows.

Consider two different spatial distributions of charge density, _a(r) and _b(r). These might be relegated to different regions, or occupy the same region. Suppose we have found the potentials _a and _b which satisfy Poisson's equation, (4.2.3), with the respective charge distributions _a and _b. By definition,

Adding these expressions, we obtain

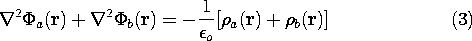
Because the derivatives called for in the Laplacian operation- for example, the second derivatives of (4.2.3)- give the same result whether they operate on the potentials and then are summed or operate on the sum of the potentials, (3) can also be written as

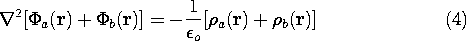
The mathematical statement of the superposition principle follows from (1) and (2) and (4). That is, if

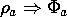
then

The potential distribution produced by the superposition of the charge distributions is the sum of the potentials associated with the individual distributions.