5.2
Uniqueness of Solutions to Poisson's Equation

We shall show in this section that a potential distribution obeying Poisson's equation is completely specified within a volume V if the potential is specified over the surfaces bounding that volume. Such a uniqueness theorem is useful for two reasons: (a) It tells us that if we have found such a solution to Poisson's equation, whether by mathematical analysis or physical insight, then we have found the only solution; and (b) it tells us what boundary conditions are appropriate to uniquely specify a solution. If there is no charge present in the volume of interest, then the theorem states the uniqueness of solutions to Laplace's equation.

Following the method "reductio ad absurdum", we assume that the solution is not unique- that two solutions, _a and _b, exist, satisfying the same boundary conditions- and then show that this is impossible. The presumably different solutions _a and _b must satisfy Poisson's equation with the same charge distribution and must satisfy the same boundary conditions.

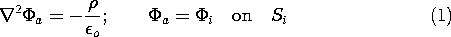
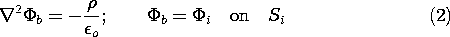
It follows that with _d defined as the difference in the two potentials, _d = _a - _b,

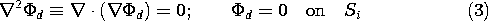
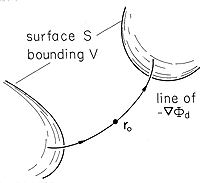
A simple argument now shows that the only way _d can both satisfy Laplace's equation and be zero on all of the bounding surfaces is for it to be zero. First, it is argued that _d cannot possess a maximum or minimum at any point within V. With the help of Fig. 5.2.1, visualize the negative of the gradient of _d, a field line, as it passes through some point r_o. Because the field is solenoidal (divergence free), such a field line cannot start or stop within V (Sec. 2.7). Further, the field defines a potential (4.1.4). Hence, as one proceeds along the field line in the direction of the negative gradient, the potential has to decrease until the field line reaches one of the surfaces S_i bounding V. Similarly, in the opposite direction, the potential has to increase until another one of the surfaces is reached. Accordingly, all maximum and minimum values of _d (r ) have to be located on the surfaces.

Figure 5.2.1 Field line originating on one part of bounding surface and terminating on another after passing through the point r_o

The difference potential at any interior point cannot assume a value larger than or smaller than the largest or smallest value of the potential on the surfaces. But the surfaces are themselves at zero potential. It follows that the difference potential is zero everywhere in V and that _a = _b. Therefore, only one solution exists to the boundary value problem stated with (1).