6.2
Laws and Continuity Conditions with Polarization

With the unpaired and polarization charge densities distinguished, Gauss' law becomes

where (6.1.6) relates 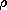_p to P.

Because P is an "averaged" polarization per unit volume, it is a "smooth" vector function of position on an atomic scale. In this sense, it is a macroscopic variable. The negative of its divergence, the polarization charge density, is also a macroscopic quantity that does not reflect the "graininess" of the microscopic charge distribution. Thus, as it appears in (1), the electric field intensity is also a macroscopic variable.

Integration of (1) over an incremental volume enclosing a section of the interface, as carried out in obtaining (1.3.7), results in

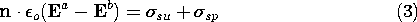
where (6.1.7) relates _sp to P.

These last two equations, respectively, give expression to the continuity condition of Gauss' law, (1), at a surface of discontinuity.

Polarization Current Density and Ampère's Law

Gauss' law is not the only one affected by polarization. If the polarization density varies with time, then the flow of charge across the surface S described in Sec. 6.1 comprises an electrical current. Thus, we need to investigate charge conservation, and more generally the effect of a time-varying polarization density on Amp\'ere's law. To this end, the following steps lead to the polarization current density implied by a time-varying polarization density.

According to the definition of P evolved in Sec. 6.1, the process of polarization transfers an amount of charge dQ

through a surface area element da. This is perhaps envisioned in terms of the volume d da shown in Fig. 6.2.1. If the polarization density P varies with time, then according to this equation, charge is passed through the area element at a finite rate. For a change in qNd, or P, of 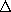P, the amount of charge that has passed through the incremental area element da is

Figure 6.2.1 Charges passing through area element da result in polarization current density.

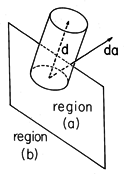
Note that we have two indicators of differentials in this expression. The d refers to the fact that Q is differential because da is a differential. The rate of change with time of dQ, (dQ)/ t, can be identified with a current di_p through da, from side (b) to side (a).

The partial differentiation symbol is used to distinguish the differentiation with respect to t from the space dependence of P.

A current di_p through an area element da is usually written as a current density dot-multiplied by da

Hence, we compare these last two equations and deduce that the polarization current density is

Note that J_p and 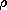_p, via (2) and (9), automatically obey a continuity law having the same form as the charge conservation equation, (2.3.3).

Hence, we can think of a rate of charge transport in a material medium as consisting of a current density of unpaired charges J_u and a polarization current density J_p, each obeying its own conservation law. This is also implied by Ampère's law, as now generalized to include the effects of polarization.

In the EQS approximation, the magnetic field intensity is not usually of interest, and so Ampère's law is of secondary importance. But if H were to be determined, J_p would make a contribution. That is, Ampère's law as given by (2.6.2) is now written with the current density divided into paired and unpaired parts. With the latter given by (9), Ampère's differential law, generalized to include polarization, is

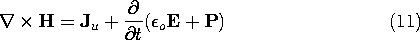
This law is valid whether quasistatic approximations are to be made or not. However, it is its implication for charge conservation that is usually of interest in the EQS approximation. Thus, the divergence of (11) gives zero on the left and, in view of (1), (2), and (9), the expression becomes

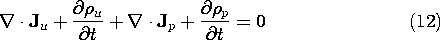
Thus, with the addition of the polarization current density to (11), the divergence of Ampère's law gives the sum of the conservation equations for polarization charges, (10), and unpaired charges

In the remainder of this chapter, it will be assumed that in the polarized material, 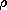_u is usually zero. Thus, (13) will not come into play until Chap. 7.

Displacement Flux Density

Primarily in dealing with field-dependent polarization phenomena, it is customary to define a combination of quantities appearing in Gauss' law and Ampère's law as the displacement flux density D.

We regard P as representing the material and E as a field quantity induced by the external sources and the sources within the material. This suggests that D be considered a "hybrid" quantity. Not all texts on electromagnetism take this point of view. Our separation of all quantities appearing in Maxwell's equations into field and material quantities aids in the construction of models for the interaction of fields with matter.

With 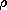_p replaced by (2), Gauss' law (1) can be written in terms of D defined by (14),

while the associated continuity condition, (3) with _sp replaced by (4), becomes

The divergence of D and the jump in normal D determine the unpaired charge densities. Equations (15) and (16) hold, unchanged in form, both in free space and matter. To adapt the laws to free space, simply set D = _o E.

Ampère's law is also conveniently written in terms of D. Substitution of (14) into (11) gives

Now the displacement current density D / t includes the polarization current density.