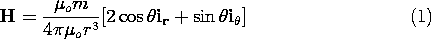
The sources of magnetic field in matter are the (more or less) aligned magnetic dipoles of individual electrons or currents caused by circulating electrons.
In Sec. 8.3, we defined the magnitude of the magnetic moment m of a circulating current loop of current i and area a as m = ia. The moment vector, m, was defined as normal to the surface spanning the contour of the loop and pointing in the direction determined by the right-hand rule. In Sec. 8.3, where the moment was in the z direction in spherical coordinates, the loop was found to produce the magnetic field intensity
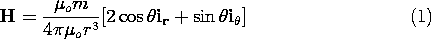
This field is analogous to the electric field associated with a dipole having the moment p. With p directed along the z axis, the electric dipole field is given by taking the gradient of (4.4.10).
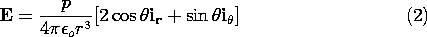
Thus, the dipole fields are obtained from each other by making the identifications
In Sec. 6.1, a spatial distribution of electric dipoles is represented by the polarization density P = Np, where N is the number density of dipoles. Similarly, here we define a magnetization density as
where again N is the number of dipoles per unit volume. Note that
just as the analog of the dipole moment p is 
o m, the
analog of the polarization density P is o M.