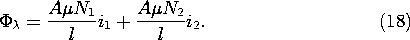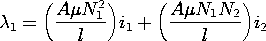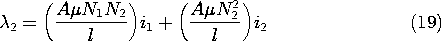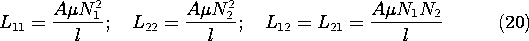9
Magnetization
9.0 Introduction
The sources of the magnetic fields considered in Chap. 8 were
conduction currents associated with the motion of unpaired charge
carriers through materials. Typically, the current was in a metal and
the carriers were conduction electrons. In this chapter, we recognize
that materials provide still other magnetic field sources. These
account for the fields of permanent magnets and for the increase in
inductance produced in a coil by insertion of a magnetizable material.
Magnetization effects are due to the propensity of the atomic
constituents of matter to behave as magnetic dipoles. It is natural
to think of electrons circulating around a nucleus as comprising a
circulating current, and hence giving rise to a magnetic moment
similar to that for a current loop, as discussed in Example 8.3.2.
More surprising is the magnetic dipole moment found for
individual electrons. This moment, associated with the electronic
property of spin, is defined as the Bohr magneton

where e/m is the electronic charge-to-mass ratio, 1.76 x
1011 coulomb/kg, and 2 \hbar is Planck's constant, \hbar =
1.05 x 10-34 joule-sec so that me has the units A -
m2. The quantum mechanics of atoms and molecules dictates that,
whether due to the orbits or to the spins, the electronic
contributions to their net dipole moments tend to cancel.
Those that do make a contribution are typically in unfilled shells.
\hbar is Planck's constant, \hbar =
1.05 x 10-34 joule-sec so that me has the units A -
m2. The quantum mechanics of atoms and molecules dictates that,
whether due to the orbits or to the spins, the electronic
contributions to their net dipole moments tend to cancel.
Those that do make a contribution are typically in unfilled shells.
An estimate of the moment that would result if each atom or
molecule of a material contributed only one Bohr magneton shows that
the orbital and spin contributions from all the electrons comprising a
typical solid had better tend to cancel or the resulting field effects
would be prodigious indeed. Even if each atom or molecule is made to
contribute only one Bohr magneton of magnetic moment, a magnetic field
results comparable to that produced by extremely large conduction
currents. To make this apparent, compare the magnetic field induced
by a current loop having a radius R and carrying a current i (Fig.
9.0.la) to that from a spherical collection of dipoles (Fig. 9.0.1b),
each having the magnetic moment of only one electron.
\fig9.0.12in(a) Current i in loop of radius R gives dipole
moment m. (b) Spherical material of radius R has dipole moment
approximated as the sum of atomic dipole moments.
In the case of the spherical material, we consider the net dipole
moment to be simply the moment me of a single molecule multiplied
by the number of molecules. The number of molecules per unit mass is
Avogadro's number (A0 = 6.023 x 1026 molecules/kg-mole)
divided by the molecular weight, Mo. The mass is the volume
multiplied by the mass density  (kg/m3).
Thus, for a sphere having radius R, the sum of the dipole moments is
(kg/m3).
Thus, for a sphere having radius R, the sum of the dipole moments is

Suppose that the current loop shown in Fig. 9.0.1a has the same
radius R as the sphere. What current i would give rise to a magnetic
moment equal to that from the sphere of hypothetical material? If the
moment of the loop, given by (8.3.19) as being m = i R2, is set
equal to that of the sphere, (2), it follows that i must be
R2, is set
equal to that of the sphere, (2), it follows that i must be

Hence, for iron (where  = 7.86 x 103 and Mo = 56) and a
radius of 10 cm, the current required to produce the same magnetic
moment is 105 A.
= 7.86 x 103 and Mo = 56) and a
radius of 10 cm, the current required to produce the same magnetic
moment is 105 A.
Material magnetization can either be permanent or be induced by
the application of a field, much as for the polarizable materials
considered in Chap. 6. In most materials, the average moment per
molecule that can be brought into play is much less than one Bohr
magneton. However, highly magnetizable materials can produce net
magnetic moments comparable to that estimated in (2).
The development of magnetization in this chapter parallels that
for polarization in Chap. 6. Just as the polarization density was
used in Sec. 6.1 to represent the effect of electric dipoles on the
electric field intensity, the magnetization density introduced in Sec.
9.1 will account for the contributions of magnetic dipoles to the
magnetic field intensity. The MQS laws and continuity conditions then
collected in Sec. 9.2 are the basis for the remaining sections, and
for Chap. 10 as well.
Because permanent magnets are so common, the permanent
magnetization fields considered in Sec. 9.3 are more familiar than the
permanent polarization electric fields of Sec. 6.3. Similarly, the
force experienced as a piece of iron is brought into a magnetic field
is common evidence of the induced magnetization described by the
constitutive laws of Sec. 9.4.
The extensive analogy between polarization and magnetization
makes most of the examples from Chap. 6 analogous to magnetization
examples. This is especially true in Secs. 9.5 and 9.6, where
materials are considered that have a magnetization that is linearly
related to the magnetic field intensity. Thus, these sections not
only build on the insights gained in the earlier sections on
polarization, but give the opportunity to expand on both topics as
well. The magnetic circuits considered in Sec. 9.7 are of great
practical interest and exemplify an approximate way for the
evaluation of fields in the presence of strongly magnetized
materials. The saturation of magnetizable materials is of primary
practical concern. The problems for Secs. 9.6 and 9.7 are an
introduction to fields in materials that are magnetically nonlinear.
We generalize Faraday's law in Sec. 9.2 so that it can be used in
this chapter to predict the voltage at the terminals of coils in
systems that include magnetization. This generalization is
used to determine terminal relations that include magnetization in Sec.
9.5. The examples in the subsequent sections study the
implications of Faraday's law with magnetization included.
As in Chap. 8, we confine ourselves in this chapter to examples that
can be modeled using the terminal variables of perfectly conducting
circuits. The MQS laws, generalized in Sec. 9.2 to include
magnetization, form the basis for the discussion of electric
fields in MQS systems that is the theme of Chap. 10.
9.1 Magnetization Density
The sources of magnetic field in matter are the (more or less)
aligned magnetic dipoles of individual electrons or currents caused by
circulating electrons.
1 Magnetic monopoles, which would play a
role with respect to magnetic fields analogous to that of the charge
with respect to electric fields, may in fact exist, but are certainly
not of engineering significance. See Science, Research News,
"In search of magnetic monopoles," Vol. 216, p. 1086 (June 4,
1982). We now describe the effect on the magnetic field of a
distribution of magnetic dipoles representing the material.
In Sec. 8.3, we defined the magnitude of the magnetic moment m of a
circulating current loop of current i and area a as m = ia.
The moment vector, m, was defined as normal to the surface spanning
the contour of the loop and pointing in the direction determined by the
right-hand rule. In
Sec. 8.3, where the moment was in the z direction in spherical
coordinates, the loop was found to produce the magnetic field
intensity
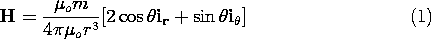
This field is analogous to the electric field
associated with a dipole having the moment p. With p directed
along the z axis, the electric dipole field is given by taking the
gradient of (4.4.10).
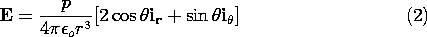
Thus, the dipole fields are obtained from each other by making the
identifications

In Sec. 6.1, a spatial distribution of electric dipoles is
represented by the polarization density P = Np, where N is the
number density of dipoles. Similarly, here we define a
magnetization density as

where again N is the number of dipoles per unit volume. Note that
just as the analog of the dipole moment p is  o m, the
analog of the polarization density P is
o m, the
analog of the polarization density P is  o M.
o M.
9.2 Laws and Continuity Conditions with Magnetization
Recall that the effect of a spatial distribution of electric
dipoles upon the electric field is described by a generalization of
Gauss' law for electric fields, (6.2.1) and (6.2.2),

The effect of the spatial distribution of magnetic dipoles upon the
magnetic field intensity is now similarly taken into account by
generalizing the magnetic flux continuity law.

In this law, there is no analog to an unpaired electric charge
density.
The continuity condition found by integrating (2) over an
incremental volume enclosing a section of an interface having a normal
n is
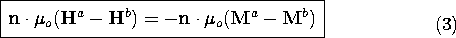
Suggested by the analogy to the description of polarization is the
definition of the quantities on the right in (2) and (3),
respectively, as the magnetic charge density 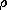 m and the
magnetic surface charge density
m and the
magnetic surface charge density  sm.
sm.

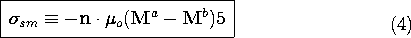
Faraday's Law Including Magnetization
The modification of the magnetic flux continuity law implies that
another of Maxwell's equations must be generalized. In introducing
the flux continuity law in Sec. 1.7, we observed that it was almost
inherent in Faraday's law. Because the divergence of the curl is
zero, the divergence of the free space form of Faraday's law
reduces to
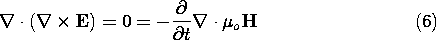
Thus, in free space,  o H must have a divergence that is at
least constant in time. The magnetic flux continuity law adds the
information that this constant is zero. In the presence of
magnetizable material, (2) shows that the quantity
o H must have a divergence that is at
least constant in time. The magnetic flux continuity law adds the
information that this constant is zero. In the presence of
magnetizable material, (2) shows that the quantity  o(H +
M ) is solenoidal. To make Faraday's law consistent with this
requirement, the law is now written as
o(H +
M ) is solenoidal. To make Faraday's law consistent with this
requirement, the law is now written as
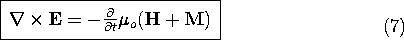
Magnetic Flux Density
The grouping of H and M in Faraday's law and the flux
continuity law makes it natural to define a new variable, the
magnetic flux density B.

This quantity plays a role that is analogous to that of the
electric displacement flux density D defined by (6.2.14).
Because there are no macroscopic quantities of monopoles of magnetic
charge, its divergence is zero. That is, the flux continuity law,
(2), becomes simply

and the corresponding continuity condition, (3), becomes simply

A similar simplification is obtained by writing Faraday's law in
terms of the magnetic flux density. Equation (7) becomes

If the magnetization is specified independent of H, it is
usually best to have it entered explicitly in the formulation by not
introducing B. However, if M is given as a function of
H, especially if it is linear in H, it is most convenient
to remove M from the formulation by using B as a variable.
Terminal Voltage with Magnetization
In Sec. 8.4, where we discussed the terminal voltage of a
perfectly conducting coil, there was no magnetization. The
generalization of Faraday's law to include magnetization requires a
generalization of the terminal relation.
The starting point in deriving the terminal relation was Faraday's
integral law, (8.4.9). This law is generalized to included
magnetization effects by replacing  o H with B.
Otherwise, the derivation of the terminal relation, (8.4.11), is
the same as before. Thus, the terminal voltage is again
o H with B.
Otherwise, the derivation of the terminal relation, (8.4.11), is
the same as before. Thus, the terminal voltage is again

but now the flux linkage is

In Sec. 9.4 we will see that Faraday's law of induction, as
reflected in these last two relations, is the basis for measuring
B.
9.3 Permanent Magnetization
As the modern-day versions of the lodestone, which made the
existence of magnetic fields apparent in ancient times, permanent
magnets are now so cheaply manufactured that they are used at home to
pin notes on the refrigerator and so reliable that they are at the
heart of motors, transducers, and information storage systems. To a
first approximation, a permanent magnet can be modeled by a material
having a specified distribution of magnetization density M. Thus,
in this section we consider the magnetic field intensity generated by
prescribed distributions of M.
In a region where there is no current density J, Ampère's law
requires that H be irrotational. It is then often convenient to
represent the magnetic field intensity in terms of the scalar magnetic
potential \Psi introduced in Sec. 8.3.

From the flux continuity law, (9.2.2), it then follows that \Psi
satisfies Poisson's equation.
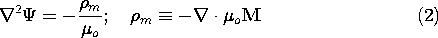
A specified magnetization density leads to a prescribed
magnetic charge density 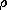 m. The situation is analogous to
that considered in Sec. 6.3, where the polarization density was
prescribed and, as a result, where
m. The situation is analogous to
that considered in Sec. 6.3, where the polarization density was
prescribed and, as a result, where 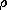 p was known.
p was known.
Of course, the net magnetic charge of a magnetizable body is always
zero, because
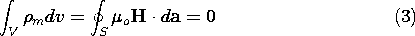
if the integral is taken over the entire volume containing the body.
Techniques for solving Poisson's equation for a prescribed charge
distribution developed in Chaps. 4
and 5 are directly applicable here. For example, if the magnetization
is given throughout all space and there are no other sources, the
magnetic scalar potential is given by a superposition integral. Just
as the integral of (4.2.2) is (4.5.3), so the integral of (2) is

If the region of interest is bounded by material on which boundary
conditions are specified, (4) provides the particular solution.
Example 9.3.1. Magnetic Field Intensity of a Uniformly Magnetized
Cylinder
The cylinder shown in Fig. 9.3.1 is uniformly magnetized in the z
direction, M = Mo iz. The first step toward finding the
resulting H within the cylinder and in the surrounding free space
is an evaluation of the distribution of magnetic charge density. The
uniform M has no divergence, so 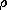 m = 0 throughout the
volume. Thus, the source of H is on the surfaces where M
originates and terminates. In view of (9.2.3), it takes the form of
the surface charge density
m = 0 throughout the
volume. Thus, the source of H is on the surfaces where M
originates and terminates. In view of (9.2.3), it takes the form of
the surface charge density
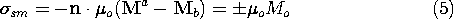
The upper and lower signs refer to the upper and lower surfaces.

In principle, we could use the superposition integral to find the
potential everywhere. To keep the integration simple, we
confine ourselves here to finding it on the z axis. The integration
of (4) then reduces to integrations over the endfaces of the
cylinder.
With absolute magnitudes used to make the expressions valid regardless
of position along the z axis, these integrals become
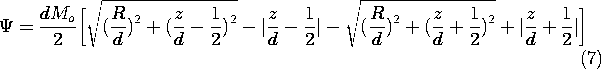
The field intensity follows from (1)
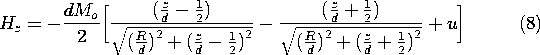
where u \equiv 0 for |z| > d/2 and u \equiv 2 for -d/2 < z <
d/2.
Here, from top to bottom, respectively, the signs correspond to
evaluating the field above the upper surface, within the magnet, and
below the bottom surface.
The axial distributions of \Psi and Hz shown in Fig. 9.3.1
are consistent with a three-dimensional picture of a field that
originates on the top face of the magnet and terminates on the bottom
face. As for the spherical magnet (the analogue of the permanently
polarized sphere shown in Fig. 6.3.1), the magnetic field intensity
inside the magnet has a direction opposite to that of M.
In practice, M would most likely be determined by making
measurements of the external field and then deducing M from this
field.
If the magnetic field intensity is generated by a combination of
prescribed currents and permanent magnetization, it can be evaluated
by superimposing the field due to the current
and the magnetization. For example, suppose that the
uniformly magnetized circular cylinder of Fig. 9.3.1 were surrounded
by the N-turn solenoid of Fig. 8.2.3. Then the axial field intensity
would be the sum of that for the current [predicted by the
Biot-Savart law, (8.2.7)], and for the magnetization [predicted
by the negative gradient of (4)].
Example 9.3.2. Retrieval of Signals Stored on Magnetizable Tape
Permanent magnetization is used for a permanent record in the
tape recorder. Currents in an electromagnet are used to induce the
permanent magnetization, exploiting the hysteresis in the
magnetization of certain materials, as will be discussed in Sec. 9.4.
Here we look at a model of perpendicular magnetization, an actively
pursued research field. The conventional recording is done by
producing magnetization M parallel to the tape.

In a thin tape at rest, the magnetization density shown in Fig. 9.3.2
is assumed to be uniform over the thickness and to be of the simple
form

The magnetic field is first determined in a frame of reference
attached to the tape, denoted by (x, y, z) as defined in Fig. 9.3.2.
The tape moves with a velocity U with respect to a fixed sensing
"head," and so our second step will be to represent this field in
terms of fixed coordinates. With Fig. 9.3.3 in view, it is clear that
these coordinates, denoted by (x' ,y' ,z' ), are
related to the moving coordinates by
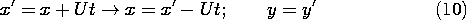
Thus, from the fixed reference frame, the magnetization takes the form
of a traveling wave.
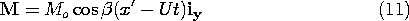
If \bf M is observed at a fixed location x', it has a sinusoidal
temporal variation with the frequency 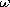 =
=  U. This relationship
between the fixed frame frequency and the spatial periodicity
suggests how the distribution of magnetization is established by "recording"
a signal having the frequency
U. This relationship
between the fixed frame frequency and the spatial periodicity
suggests how the distribution of magnetization is established by "recording"
a signal having the frequency 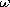 .
.

The magnetization density has no divergence in the volume of the
tape, so the field source is a surface charge density. With upper and
lower signs denoting the upper and lower tape surfaces, it follows
that

The continuity conditions to be satisfied at the upper and lower
surfaces represent the continuity of magnetic flux
(9.2.3)
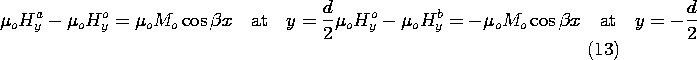
and the continuity of tangential \bf H
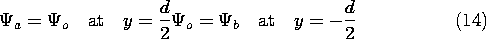
In addition, the field should go to zero as y  \pm
\pm  .
.
Because the field sources are confined to surfaces, the magnetic
scalar potential must satisfy Laplace's equation, (2) with 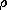 m =
0, in the
bulk regions delimited by the interfaces. Motivated by the "odd"
symmetry of the source with respect to the y = 0 plane and its
periodicity in x, we pick solutions to Laplace's equation for the
magnetic potential above (a), inside (o), and below (b) the tape that
also satisfy the odd symmetry condition of having \Psi (y) = - \Psi
(-y).
m =
0, in the
bulk regions delimited by the interfaces. Motivated by the "odd"
symmetry of the source with respect to the y = 0 plane and its
periodicity in x, we pick solutions to Laplace's equation for the
magnetic potential above (a), inside (o), and below (b) the tape that
also satisfy the odd symmetry condition of having \Psi (y) = - \Psi
(-y).
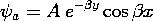

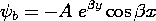
Subject to the requirement that  > 0, the exterior potentials go to
zero at y = \pm
> 0, the exterior potentials go to
zero at y = \pm 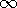 . The interior function is made an odd function
of y by excluding the cosh (
. The interior function is made an odd function
of y by excluding the cosh ( y) cos (
y) cos ( x) solution to
Laplace's equation, while the exterior functions are made odd by making the
coefficients equal in magnitude and opposite in sign. Thus, only two
coefficients remain to be determined. These follow from substituting
the assumed solution into either of (13) and either
of (14), and then solving the two equations to obtain
x) solution to
Laplace's equation, while the exterior functions are made odd by making the
coefficients equal in magnitude and opposite in sign. Thus, only two
coefficients remain to be determined. These follow from substituting
the assumed solution into either of (13) and either
of (14), and then solving the two equations to obtain
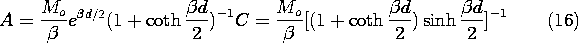
The conditions at one interface are automatically satisfied if
those at the other are met. This is a proof that the assumed
solutions have indeed been correct. Our foresight in defining
the origin of the y axis to be at the symmetry plane and exploiting
the resulting odd dependence of \Psi on y has reduced the number of
undetermined coefficients from four to two.
This field is now expressed in the fixed frame coordinates.
With A defined by (16a) and x and y given in terms of the fixed
frame coordinates by (10), the magnetic potential above the tape has
been determined to be
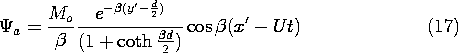
Next, we determine the output voltage of a fixed coil,
positioned at a height h above the tape, as shown in Fig. 9.3.3. This
detecting "head" has N turns, a length l in the x'
direction, and width w in the z direction. With the objective of
finding the flux linkage, we use (17) to determine the y-directed
flux density in the neighborhood of the coil.
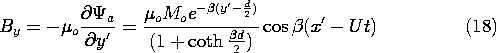
The flux linkage follows by multiplying the number of turns N
times By integrated over the surface in the plane y = h + 1\over
2 d spanned by the coil.
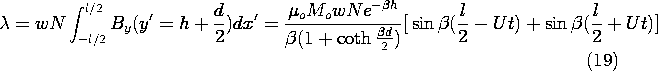
The dependence on l is clarified by using a trigonometric identity
to simplify the last term in this expression.
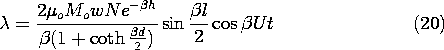
Finally, the output voltage follows from (9.2.12).
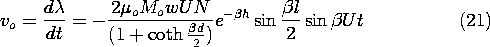
The strong dependence of this expression on the wavelength of the
magnetization, 2 /
/ , reflects the nature of fields predicted
using Laplace's equation. It follows from (21) that the output
voltage has the angular frequency
, reflects the nature of fields predicted
using Laplace's equation. It follows from (21) that the output
voltage has the angular frequency 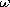 =
=  U. Thus, (21)
can also be regarded as giving the frequency
response of the sensor. The magnitude of vo has the dependence on
either the normalized
U. Thus, (21)
can also be regarded as giving the frequency
response of the sensor. The magnitude of vo has the dependence on
either the normalized  or
or 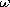 shown in Fig. 9.3.4.
shown in Fig. 9.3.4.

Two phenomena underlie the voltage response. The periodic
dependence reflects the relationship between the length l of the
coil and the wavelength 2 /
/ of the magnetization. When the
coil length is equal to the wavelength, there is as much positive as
negative flux linking the coil at a given instant, and the signal falls
to zero. This is also the condition when l is any multiple of a
wavelength and accounts for the sin (
of the magnetization. When the
coil length is equal to the wavelength, there is as much positive as
negative flux linking the coil at a given instant, and the signal falls
to zero. This is also the condition when l is any multiple of a
wavelength and accounts for the sin (
 l) term in
(21).
l) term in
(21).
The strong decay of the envelope of the output signal as the
frequency is increased, and hence the wavelength decreased, reflects a
property of Laplace's equation that frequently comes into play in
engineering electromagnetic fields. The shorter the wavelength, the
more rapid the decay of the field in the direction perpendicular to
the tape. With the sensing coil at a fixed height above the tape,
this means that once the wavelength is on the order of 2 h, there
is an essentially exponential decrease in signal with increasing
frequency. Thus, there is a strong incentive to place the coil as
close to the tape as possible.
h, there
is an essentially exponential decrease in signal with increasing
frequency. Thus, there is a strong incentive to place the coil as
close to the tape as possible.
We should expect that if the tape is very thin compared to the
wavelength, the field induced by magnetic surface charges on the top
surface would tend to be canceled by those of opposite sign on the
surface just below. This effect is accounted for by the term
[1 + \coth (
 d)] in the denominator of (21).
d)] in the denominator of (21).
In a practical recording device, the sensing head of the previous
example would incorporate magnetizable materials. To predict how
these affect the fields, we need a law relating the field to the
magnetization it induces. This is the subject of the next section.
9.4 Magnetization Constitutive Laws
The permanent magnetization model of Sec. 9.3 is a somewhat
artificial example of the magnetization density M specified,
independent of the magnetic field intensity. Even in the best of
permanent magnets, there is actually some dependence of M on
H.
Constitutive laws relate the magnetization density M or the
magnetic flux density B to the macroscopic H within a
material. Before discussing some of the more common relations and
their underlying physics, it is well to have in view an experiment
giving direct evidence of the constitutive law of magnetization. The
objective is to observe the establishment of H by a current in
accordance with Ampère's law, and deduce B from the voltage it
induces in accordance with Faraday's law.

Example 9.4.1. Toroidal Coil
A coil of toroidal geometry is shown in Fig. 9.4.1. It consists
of a donut-shaped core filled with magnetizable material with N1
turns tightly wound on its periphery. By means of a source driving
its terminals, this coil carries a current i. The resulting
current distribution can be assumed to be so smooth that the
fine structure of the field, caused by the finite size of the wires,
can be disregarded. We will ignore the slight pitch of the coil and
the associated small current component circulating around the axis of
the toroid.
Because of the toroidal geometry, the H field in the magnetizable
material is determined by Ampère's law and symmetry considerations.
Symmetry about the toroidal axis suggests that H is  directed. The integral MQS form of Ampère's law is written for a
contour C circulating about the toroidal axis within the core and at a
radius r. Because the major radius R of the torus is large compared
to the minor radius
directed. The integral MQS form of Ampère's law is written for a
contour C circulating about the toroidal axis within the core and at a
radius r. Because the major radius R of the torus is large compared
to the minor radius  w, we will ignore the variation of
r over the cross-section of the torus and approximate r by an
average radius R. The surface S spanned by this contour and shown
in Fig. 9.4.2 is pierced N1 times by the current i, giving a total
current of N1 i. Thus, the azimuthal field inside the core is
essentially
w, we will ignore the variation of
r over the cross-section of the torus and approximate r by an
average radius R. The surface S spanned by this contour and shown
in Fig. 9.4.2 is pierced N1 times by the current i, giving a total
current of N1 i. Thus, the azimuthal field inside the core is
essentially
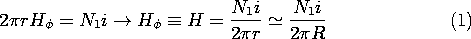
Note that the same argument shows that the magnetic field intensity
outside the core is zero.

In general, if we are given the current distribution and wish to
determine H, recourse must be made not only to Ampère's law but to
the flux continuity condition as well. In the idealized toroidal
geometry, where the flux lines automatically close on themselves
without leaving the magnetized material, the flux continuity condition
is automatically satisfied. Thus, in the toroidal configuration, the
H imposed on the core is determined by a measurement of the
current i and the geometry.
How can we measure the magnetic flux density in the core?
Because B appears in Faraday's law of induction, the measurement
of the terminal voltage of an additional coil, having N2 turns
also wound on the donut-shaped core, gives information on B. The
terminals of this coil are terminated in a high enough impedance so that
there is a negligible current in this second winding. Thus, the H
field established by the current i remains unaltered.
The flux linked by each turn of the sensing coil is essentially
the flux density multiplied by the cross-sectional area  w2/4
of the core. Thus, the flux linked by the terminals of the sensing
coil is
w2/4
of the core. Thus, the flux linked by the terminals of the sensing
coil is

and flux density in the core material is directly reflected in the
terminal flux-linkage.
The following demonstration shows how (1) and (2) can be used to
infer the magnetization characteristic of the core material from
measurement of the terminal current and voltage of the first and
second coils.
Demonstration 9.4.1. Measurement of B-H Characteristic
The experiment shown in Fig. 9.4.3 displays the magnetization
characteristic on the oscilloscope. The magnetizable material is in
the donut-shaped toroidal configuration of Example 9.4.1 with the
N1-turn coil driven by a current i from a Variac. The voltage
across a series resistance then gives a horizontal deflection of the
oscilloscope proportional to H, in accordance with (1).

The terminals of the N2 turn-coil are connected through an
integrating network to the vertical deflection terminals of the
oscilloscope. Thus, the vertical deflection is proportional to the
integral of the terminal voltage, to 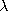 , and hence through (2),
to B.
, and hence through (2),
to B.
In the discussions of magnetization characteristics which follow,
it is helpful to think of the material as comprising the core of the
torus in this experiment. Then the magnetic field intensity H
is proportional to the current i, while the magnetic flux density B
is reflected in the voltage induced in a coil linking this flux.
Many materials are magnetically linear in the sense that

Here 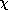 m is the magnetic susceptibility. More commonly,
the constitutive law for a magnetically linear material is written in
terms of the magnetic flux density, defined by (9.2.8).
m is the magnetic susceptibility. More commonly,
the constitutive law for a magnetically linear material is written in
terms of the magnetic flux density, defined by (9.2.8).
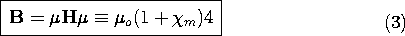
According to this law, the magnetization is taken into account
by replacing the permeability of free space  o
by the permeability
o
by the permeability  of the material. For
purposes of comparing the magnetizability of materials,
the relative permeability
of the material. For
purposes of comparing the magnetizability of materials,
the relative permeability  /
/ o is often used.
o is often used.
Typical susceptibilities for certain elements, compounds, and
common materials are given in Table 9.4.1.
Most common materials are only slightly magnetizable. Some substances
that are readily polarized, such as water, are not easily magnetized.
Note that the magnetic susceptibility can be either positive or
negative and that there are some materials, notably iron and its
compounds, in which it can be enormous. In establishing an
appreciation for the degree of magnetizability that can be expected of
a material, it is helpful to have a qualitative picture of its
microscopic origins, beginning at the atomic level but including the
collective effects of groups of atoms or molecules that result when
they become as densely packed as they are in solids. These latter
effects are prominent in the most easily magnetized materials.

The magnetic moment of an atom (or molecule) is the sum of the
orbital and spin contributions. Especially in a gas, where the atoms
are dilute, the magnetic susceptibility results from the (partial)
alignment of the individual magnetic moments by a magnetic field.
Although the spin contributions to the moment tend to cancel,
many atoms have net moments of one or more Bohr magnetons. At room
temperature, the orientations of the moments are mostly randomized by
thermal agitation, even under the most intense fields. As a result,
an applied field can give rise to a significant magnetization only at
very low temperatures. A paramagnetic material displays an
appreciable susceptibility only at low temperatures.
If, in the absence of an applied field, the spin
contributions to the moment of an atom very nearly cancel, the
material can be diamagnetic, in the sense that it displays a
slightly negative susceptibility. With the application of a field,
the orbiting electrons are slightly altered in their circulations,
giving rise to changes in moment in a direction opposite to that of
the applied field. Again, thermal energy tends to disorient these
moments. At room temperature, this effect is even smaller than that
for paramagnetic materials.
At very low temperatures, it is possible to raise the applied
field to such a level that essentially all the moments are aligned.
This is reflected in the saturation of the flux density B, as
shown in Fig. 9.4.4. At low field intensity, the slope of the
magnetization curve is  , while at high field strengths, there are
no more moments to be aligned and the slope is
, while at high field strengths, there are
no more moments to be aligned and the slope is  o. As long
as the field is raised and lowered at a rate slow enough so that
there is time for the thermal energy to reach an equilibrium with the
magnetic field, the B-H curve is single valued in the sense that
the same curve is followed whether the magnetic field is increasing
or decreasing, and regardless of its rate of change.
o. As long
as the field is raised and lowered at a rate slow enough so that
there is time for the thermal energy to reach an equilibrium with the
magnetic field, the B-H curve is single valued in the sense that
the same curve is followed whether the magnetic field is increasing
or decreasing, and regardless of its rate of change.

Until now, we have been considering the magnetization of materials
that are sufficiently dilute so that the atomic moments do not
interact with each other. In solids, atoms can be so closely spaced
that the magnetic field due to the moment of one atom can have a
significant effect on the orientation of another. In
ferromagnetic materials, this mutual interaction is all important.
To appreciate what makes certain materials ferromagnetic rather
than simply paramagnetic, we need to remember that the electrons which
surround the nuclei of atoms are assigned by quantum mechanical
principles to layers or "shells." Each shell has a particular maximum
number of electrons. The electron behaves as if it possessed a net
angular momentum, or spin, and hence a magnetic moment. A filled
shell always contains an even number of electrons which are
distributed spatially in such a manner that the total spin, and
likewise the magnetic moment, is zero.
For the majority of atoms, the outermost shell is unfilled, and so
it is the outermost electrons that play the major role in determining
the net magnetic moment of the atom. This picture of the atom is
consistent with paramagnetic and diamagnetic behavior. However, the
transition elements form a special class. They have unfilled
inner shells, so that the electrons responsible for the net moment
of the atom are surrounded by the electrons that interact most
intimately with the electrons of a neighboring atom. When such atoms
are as closely packed as they are in solids, the combination of the
interaction between magnetic moments and of electrostatic coupling
results in the spontaneous alignment of dipoles, or
ferromagnetism. The underlying interaction between atoms is both
magnetic and electrostatic, and can be understood only by invoking
quantum mechanical arguments.
In a ferromagnetic material, atoms naturally establish an array of
moments that reinforce. Nevertheless,
on a macroscopic scale, ferromagnetic materials are not
necessarily permanently magnetized. The spontaneous alignment of
dipoles is commonly confined to microscopic regions, called domains.
The moments of the individual domains are randomly oriented and cancel
on a macroscopic scale.
Macroscopic magnetization occurs when a field is applied to a
solid, because those domains that have a magnetic dipole moment nearly
aligned with the applied field grow at the expense of domains whose
magnetic dipole moments are less aligned with the applied field. The
shift in domain structure caused by raising the applied field from one
level to another is illustrated in Fig. 9.4.5. The domain walls
encounter a resistance to propagation that balances the effect of the
field.

A typical trajectory traced out in the B-H plane as the field is
applied to a typical ferromagnetic material is shown in Fig. 9.4.6.
If the magnetization is zero at the outset, the initial trajectory
followed as the field is turned up starts at the origin. If the field
is then turned down, the domains require a certain degree of coercion
to reduce their average magnetization. In fact, with the applied
field turned off, there generally remains a flux density, and the field
must be reversed to reduce the flux density to zero. The trajectory
traced out if the applied field is slowly cycled between positive and
negative values many times is the one shown in the figure, with the
remanence flux density Br when H = 0 and a
coercive field intensity Hc required to make the flux density
zero. Some values of these parameters, for materials used to
make permanent magnets, are given in Table 9.4.2.


In the toroidal geometry of Example 9.4.1, H is proportional to
the terminal current i. Thus, imposition of a sinusoidally varying
current results in a sinusoidally varying H, as illustrated in Fig.
9.4.6b. As the i and hence H increases, the trajectory in the
B-H plane is the one of increasing H. With decreasing H, a
different trajectory is followed. In general, it is
not possible to specify B simply by giving H (or even the time
derivatives of H). When the magnetization state reflects the previous
states of magnetization, the material is said to be hysteretic.
The B-H trajectory representing the response to a sinusoidal H is then
called the hysteresis loop.
Hysteresis can be both harmful and useful. Permanent
magnetization is one result of hysteresis, and as we illustrated in
Example 9.3.2, this can be the basis for the storage of information on
tapes. When we develop a picture of energy dissipation in Chap. 11,
it will be clear that hysteresis also implies the generation of heat,
and this can impose limits on the use of magnetizable materials.
Liquids having significant magnetizabilities have been synthesized
by permanently suspending macroscopic particles composed of single
ferromagnetic domains. Here also the relatively high magnetizability
comes from the ferromagnetic character of the individual domains.
However, the very different way in which the domains interact with
each other helps in gaining an appreciation for the magnetization of
ferromagnetic polycrystalline solids.
In the absence of a field imposed on the synthesized liquid, the
thermal molecular energy randomizes the dipole moments and there is no
residual magnetization. With the application of a low frequency
H field, the suspended particles assume an average alignment with the
field and a single-valued B-H curve is traced out, typically as shown
in Fig. 9.4.4. However, as the frequency is raised, the reorientation
of the domains lags behind the applied field, and the B-H curve shows
hysteresis, much as for solids.
Although both the solid and the liquid can show hysteresis, the
two differ in an important way. In the solid, the magnetization shows
hysteresis even in the limit of zero frequency. In the liquid,
hysteresis results only if there is a finite rate of change of the
applied field.
Ferromagnetic materials such as iron are metallic solids and
hence tend to be relatively good electrical conductors. As we will
see in Chap. 10, this means that unless care is taken to interrupt
conduction paths in the material, currents will be induced by a
time-varying magnetic flux density. Often, these eddy currents
are undesired. With the objective of obtaining a highly magnetizable
insulating material, iron atoms can be combined into an oxide crystal.
Although the spontaneous interaction between molecules that
characterizes ferromagnetism is indeed observed, the alignment of
neighbors is antiparallel rather than parallel. As a result, such pure
oxides do not show strong magnetic properties. However, a mixed-oxide
material like Fe3O4 (magnetite) is composed of sublattice
oxides of differing moments. The spontaneous antiparallel alignment
results in a net moment. The class of relatively magnetizable but
electrically insulating materials are called ferrimagnetic.
Our discussion of the origins of magnetization began at the
atomic level, where electronic orbits and spins are fundamental.
However, it ends with a discussion of constitutive laws that can only
be explained by bringing in additional effects that occur on scales
much greater than atomic or molecular. Thus, the macroscopic B
and H used to describe magnetizable materials
can represent averages with respect to scales of domains or of
macroscopic particles. In Sec. 9.5 we will make an artificial
diamagnetic material from a matrix of "perfectly" conducting
particles. In a time-varying magnetic field, a magnetic moment is
induced in each particle that tends to cancel that being imposed, as
was shown in Example 8.4.3. In fact, the currents induced in the
particles and responsible for this induced moment are analogous to the
induced changes in electronic orbits responsible on the atomic scale
for diamagnetism[1].
9.5 Fields In The Presence Of Magnetically Linear Insulating Materials
In this and the next two sections, we study materials with the
linear magnetization characteristic of (9.4.4). With the
understanding that  is a prescribed function of position,
B =
is a prescribed function of position,
B =  H, the MQS forms of Ampère's law and the flux
continuity law are
H, the MQS forms of Ampère's law and the flux
continuity law are


In this chapter, we assume that the current density J is confined
to perfect conductors. We will find in Chap. 10 that a time-varying
magnetic flux implies an electric field. Thus, wherever a conducting
material finds itself in a time-varying field, there is the possibility
that eddy currents will be induced. It is for this reason that
the magnetizable materials considered in this and the next sections
are presumed to be insulating. If the fields of interest
vary slowly enough, these induced currents can be negligible.
Ferromagnetic materials are often metallic, and hence also
conductors. However, materials can be made both readily magnetizable
and insulating by breaking up the conduction paths. By engineering at
the molecular or domain scale, or even introducing laminations of
magnetizable materials, the material is rendered essentially free of a
current density J. The considerations that determine the
thickness of laminations used in transformers to prevent eddy
currents will be taken up in Chap. 10.
In the regions outside the perfect conductors carrying the
current J of (1), H is irrotational and B is solenoidal.
Thus, we have a choice of representations. Either, as in Sec. 8.3, we
can use the scalar magnetic potential and let H = -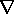 \Psi,
or we can follow the lead from Sec. 8.6 and use the vector potential
to represent the flux density by letting B =
\Psi,
or we can follow the lead from Sec. 8.6 and use the vector potential
to represent the flux density by letting B = 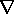 x A.
x A.
Where there are discontinuities in the permeability and/or thin
coils modeled by surface currents, the continuity conditions
associated with Ampère's law and the flux continuity law are used.
With B expressed using the linear magnetization constitutive law,
(1.4.16) and (9.2.10) become


The classification of physical configurations given in Sec. 6.5
for linearly polarizable materials is equally useful here. In the
first of these, the region of interest is of uniform permeability.
The laws summarized by (1) and (2) are the same as for free space
except that  o is replaced by
o is replaced by  , so the results of Chap. 6
apply directly. Configurations made up of materials having
essentially uniform permeabilities are of the greatest practical
interest by far. Thus, piece-wise uniform systems are the theme of
Secs. 9.6 and 9.7. The smoothly inhomogeneous systems that are the
last category in Fig. 9.5.1 are of limited practical interest.
However, it is sometimes useful, perhaps in numerical simulations, to
regard the uniform and piece-wise uniform systems as special cases of
the smoothly nonuniform systems.
, so the results of Chap. 6
apply directly. Configurations made up of materials having
essentially uniform permeabilities are of the greatest practical
interest by far. Thus, piece-wise uniform systems are the theme of
Secs. 9.6 and 9.7. The smoothly inhomogeneous systems that are the
last category in Fig. 9.5.1 are of limited practical interest.
However, it is sometimes useful, perhaps in numerical simulations, to
regard the uniform and piece-wise uniform systems as special cases of
the smoothly nonuniform systems.

\sectnonumInductance in the Presence of Linearly Magnetizable
Materials
In the presence of linearly magnetizable materials, the magnetic
flux density is again proportional to the excitation currents. If
fields are produced by a single perfectly conducting coil, its
inductance is the generalization of that introduced with (8.4.13).

The surface S spanning a contour defined by the perfectly conducting
wire is the same as that shown in Figs. 8.4.3 and 8.4.4. The effect
of having magnetizable material is, of course, represented in (5) by
the effect of this material on the intensity, direction, and
distribution of B =  H.
H.
For systems in the first category of Fig. 9.5.1, where the entire
region occupied by the field is filled by a material of uniform
permeability  , the effect of the magnetization on the inductance
is clear. The solutions to (1) and (2) for H are not altered in
the presence of the permeable material. It then follows from (5)
that the inductance is simply proportional to
, the effect of the magnetization on the inductance
is clear. The solutions to (1) and (2) for H are not altered in
the presence of the permeable material. It then follows from (5)
that the inductance is simply proportional to  .
.
Because it imposes a magnetic field intensity that never leaves
the core material, the toroid of Example 9.4.1 is a special case of a
piece-wise uniform magnetic material that acts as if all of space were
filled with the magnetizable material. As shown by the following
example, the inductance of the toroid is therefore also proportional
to  .
.
Example 9.5.1. Inductance of a Toroid
If the toroidal core of the winding shown in Fig. 9.4.1 and used
in the experiment of Fig. 9.4.3 were made a linearly magnetizable
material, what would be the voltage needed to supply the driving
current i? If we define the flux linkage of the driving coil as
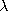 1,
1,

We now find the inductance L, where 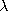 1 = Li, and hence
determine the required input voltage.
1 = Li, and hence
determine the required input voltage.
The flux linked by one turn of the driving coil is essentially
the cross-sectional area of the toroid multiplied by the flux density.
The total flux linked is this quantity multiplied by the total turns
N1.

According to the linear constitutive law, the flux density
follows from the field intensity as B =  H. For the toroid,
H is related to the driving current i by (9.4.1), so
H. For the toroid,
H is related to the driving current i by (9.4.1), so

The desired relation is the combination of these last two expressions.
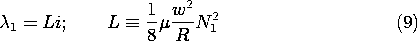
As predicted, the inductance is proportional to  . Although
inductances are generally increased by bringing paramagnetic and
especially ferromagnetic materials into their fields, the effect of
introducing ferromagnetic materials into coils can be less dramatic
than in the toroidal geometry for reasons discussed in Sec. 9.6.
The dependence of the inductance on the square of the turns results
because not only is the field induced by the current i proportional
to the number of turns, but so too is the amount of the resulting flux
that is linked by the coil.
. Although
inductances are generally increased by bringing paramagnetic and
especially ferromagnetic materials into their fields, the effect of
introducing ferromagnetic materials into coils can be less dramatic
than in the toroidal geometry for reasons discussed in Sec. 9.6.
The dependence of the inductance on the square of the turns results
because not only is the field induced by the current i proportional
to the number of turns, but so too is the amount of the resulting flux
that is linked by the coil.
Example 9.5.2. An Artificial Diamagnetic Material
The cross-section of a long (ideally "infinite") solenoid filled
with material of uniform permeability is shown in Fig. 9.5.2a. The
azimuthal surface current K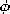 results in an axial magnetic
field intensity Hz = K
results in an axial magnetic
field intensity Hz = K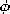 . We presume that the axial length d
is very large compared to the radius a of the coil. Thus, the field
inside the coil is uniform while that outside is zero. To see that
this simple field solution is indeed correct, note that it is both
irrotational and solenoidal everywhere except at the surface r = a, and
that there the boundary conditions, (3) and (4), are
satisfied.
. We presume that the axial length d
is very large compared to the radius a of the coil. Thus, the field
inside the coil is uniform while that outside is zero. To see that
this simple field solution is indeed correct, note that it is both
irrotational and solenoidal everywhere except at the surface r = a, and
that there the boundary conditions, (3) and (4), are
satisfied.

For an n-turn coil carrying a current i, the surface current
density K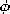 = ni/d. Thus, the magnetic field intensity is
related to the terminal current by
= ni/d. Thus, the magnetic field intensity is
related to the terminal current by

In the linearly magnetized core region, the flux density is
Bz =  Hz, and so it is also uniform. As a result, the flux
linked by each turn is simply
Hz, and so it is also uniform. As a result, the flux
linked by each turn is simply  a2 Bz and the total flux linked
by the coil is
a2 Bz and the total flux linked
by the coil is

Substitution from (1) then gives
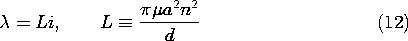
where L is the inductance of the coil. Because the coil is assumed
to be very long, its inductance is increased by a factor  /
/ o
over that of a coil in free space, much as for the toroid of Example
9.5.1.
o
over that of a coil in free space, much as for the toroid of Example
9.5.1.
Now suppose that the permeable material is actually a cubic
array of metal spheres, each having a radius R, as shown in Fig.
9.5.2b. The frequency of the current i is presumably high enough
so that
each sphere can be regarded as perfectly conducting in the MQS sense
discussed in Sec. 8.4. The spacing s of the spheres is large compared
to their radius, so that the field of one sphere does not produce an
appreciable field at the positions of its neighbors. Each sphere
finds itself in an essentially uniform magnetic field.
The dipole moment of the currents induced in a sphere by a
magnetic field that is uniform at infinity was calculated in Example
8.4.3, (8.4.21).

Because the induced currents must produce a field that
bucks out the imposed field, a negative moment is induced by a
positive field.
By definition, the magnetization density is the number of magnetic
moments per unit volume. For a cubic array with spacing s
between the sphere centers, the number per unit volume is s-3.
Thus, the magnetization density is simply
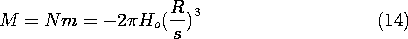
Comparison of this expression to (9.4.3), which defines the
susceptibility 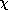 m, shows that
m, shows that

As we might have expected from the antiparallel moment induced in a
sphere by an imposed field, the susceptibility is negative. The
permeability, related to 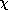 m by (9.4.4), is therefore less than
1.
m by (9.4.4), is therefore less than
1.
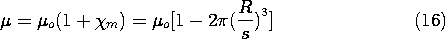
The perfectly conducting spheres effectively reduce the
cross-sectional area of the flux, as suggested by Fig. 9.5.3, and
hence reduce the inductance. With the introduction of the array of
metal spheres, the inductance goes from a value given by (12) with
 =
=  o to one with
o to one with  given by (16).
given by (16).

Faraday's law of induction is also responsible for diamagnetism due
to atomic moments. Instead of inducing circulating conduction
currents in a metal sphere, as in this example, the time-varying
field induces changes in the orbits of electrons about the nucleus
that, on the average, contribute an antiparallel magnetic moment to the
atom.
The following demonstration is the MQS analog of the EQS
Demonstration 6.6.1. In the latter, a measurement was made of the
change in capacitance caused by inserting an artificial dielectric
between capacitor plates. Here the change in inductance is observed
as an artificial diamagnetic material is inserted into a solenoid.
Although the spheres are modeled as perfectly conducting in both
demonstrations, we will find in Chap. 10 that the requirements
to justify this assumption in this MQS example are very different from
those for its EQS counterpart.
Demonstration 9.5.1. Artificial Diamagnetic Material
The experiment shown in Fig. 9.5.4 measures
the change in solenoid inductance when an array of conducting spheres
is inserted. The coil is driven at the angular frequency 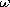 by an
oscillator-amplifier. Over the length d shown
in the figure, the field tends to be uniform. The circuit shown
schematically in Fig. 9.5.5 takes the form of a bridge with the
inductive reactance of L2 used to balance the reactance of the
central part of the empty solenoid.
by an
oscillator-amplifier. Over the length d shown
in the figure, the field tends to be uniform. The circuit shown
schematically in Fig. 9.5.5 takes the form of a bridge with the
inductive reactance of L2 used to balance the reactance of the
central part of the empty solenoid.


The input resistances of the oscilloscope's balanced amplifiers,
represented by Rs, are large compared to the inductor reactances.
These branches dominate over the inductive reactances in determining
the current through the inductors and, as a result, the inductor
currents remain essentially constant as the inductances are varied.
With the reactance of the inductor L2 balancing that of the empty
solenoid, these currents are equal and the balanced amplifier voltage
vo = 0. When the array of spheres is inserted into the solenoid,
the currents through both legs remain essentially constant. Thus, the
resulting voltage vo is the change in voltage across the solenoid
caused by its change in inductance 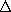 L.
L.
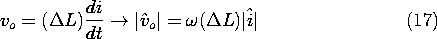
In the latter expression, the current and voltage indicated by a
circumflex are either peak or
rms sinusoidal steady state amplitudes. In view of (12), this
expression becomes
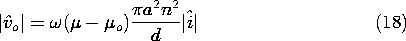
In terms of the sphere radius and spacing, the change in permeability
is given by (16), so the voltage measured by the balanced amplifiers
is
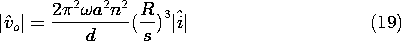
To evaluate this expression, we need only the frequency and amplitude
of the coil current, the number of turns in the length d, and other
dimensions of the system.
Induced Magnetic Charge: Demagnetization
The complete analogy between linearly polarized and linearly
magnetized materials is profitably carried yet another step.
Magnetic charge is induced where  is spatially varying, and
hence the magnetizable material can introduce sources that revise
the free space field distribution. In the linearly magnetizable
material, the distribution of these sources is not known until after
the fields have been determined. However, it is often helpful in
qualitatively predicting the field effects of magnetizable materials
to picture the distribution of induced magnetic charges.
is spatially varying, and
hence the magnetizable material can introduce sources that revise
the free space field distribution. In the linearly magnetizable
material, the distribution of these sources is not known until after
the fields have been determined. However, it is often helpful in
qualitatively predicting the field effects of magnetizable materials
to picture the distribution of induced magnetic charges.
Using a vector identity, (2) can be written

Rearrangement of this expression shows that the source of
 oH, the magnetic charge density, is
oH, the magnetic charge density, is
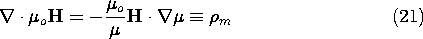
Most often we deal with piece-wise uniform systems where variations in
 are confined to interfaces. In that case, it is appropriate to
write the continuity of flux density condition in the form
are confined to interfaces. In that case, it is appropriate to
write the continuity of flux density condition in the form
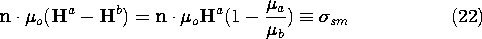
where  sm is the magnetic surface charge density. The
following illustrates the use of this relation.
sm is the magnetic surface charge density. The
following illustrates the use of this relation.
Illustration. The Demagnetization Field
A sphere of material having uniform permeability  is placed
in an initially uniform upward-directed field. It is clear from
(21) that there are no distortions of the uniform field from magnetic
charge induced in the volume of the material. Rather, the sources of
induced field are located on the surface where the imposed field has a
component normal to the permeability discontinuity. It follows from
(22) that positive and negative magnetic surface charges are induced
on the top and bottom parts of the surface, respectively.
is placed
in an initially uniform upward-directed field. It is clear from
(21) that there are no distortions of the uniform field from magnetic
charge induced in the volume of the material. Rather, the sources of
induced field are located on the surface where the imposed field has a
component normal to the permeability discontinuity. It follows from
(22) that positive and negative magnetic surface charges are induced
on the top and bottom parts of the surface, respectively.
The H field caused by the induced magnetic surface charges
originates at the positive charge at the top and terminates on the
negative charge at the bottom. This is illustrated by the
magnetization analog of the permanently polarized sphere, considered
in Example 6.3.1. Our point here is that the field resulting from
these induced magnetic surface charges tends to cancel the one
imposed. Thus, the field intensity available to magnetize the
material is reduced.
The remarks following (6.5.11) apply equally well here. The
roles of E, D, and  are taken by H,
B, and
are taken by H,
B, and  . In regions of uniform permeability, (1) and (2)
are the same laws considered in Chap. 8, and where the current
density is zero, Laplace's equation governs. As we now consider
piece-wise nonuniform systems, the effect of the material is
accounted for by the continuity conditions.
. In regions of uniform permeability, (1) and (2)
are the same laws considered in Chap. 8, and where the current
density is zero, Laplace's equation governs. As we now consider
piece-wise nonuniform systems, the effect of the material is
accounted for by the continuity conditions.
9.6 Fields in Piece-Wise Uniform Magnetically Linear Materials
Whether we choose to represent the magnetic field in terms of the
magnetic scalar potential \Psi or the vector potential A, in a
current-free region having uniform permeability it assumes a
distribution governed by Laplace's equation. That is, where  is
constant and J = 0, (9.5.1) and (9.5.2) require that H is
both solenoidal and irrotational. If we let H = -
is
constant and J = 0, (9.5.1) and (9.5.2) require that H is
both solenoidal and irrotational. If we let H = -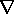 \Psi,
the field is automatically irrotational and
\Psi,
the field is automatically irrotational and

is the condition that it be solenoidal. If we let
 H =
H = 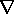 x A, the field is automatically
solenoidal. The condition that it also be irrotational (together
with the requirement that A be solenoidal) is
then
x A, the field is automatically
solenoidal. The condition that it also be irrotational (together
with the requirement that A be solenoidal) is
then
A = 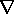 (\nabla
(\nabla  A) -
A) - 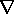 2 A
2 A

Thus, in Cartesian coordinates, each component of A satisfies the
same equation as does \Psi.
The methods illustrated for representing piece-wise uniform
dielectrics in Sec. 6.6 are applicable here as well. The major
difference is that here, currents are used to excite the field whereas
there, unpaired charges were responsible for inducing the polarization.
The sources are
now the current density and surface current density rather than
unpaired volume and surface charges. Thus, the external excitations
drive the curl of the field, in accordance with (9.5.1) and (9.5.3),
rather than its divergence.
The boundary conditions needed at interfaces between magnetically
linear materials are

for the normal component of the magnetic field intensity, and

for the tangential component, in the presence of a surface current.
As before, we shall find it convenient to represent windings by
equivalent surface currents.
Example 9.6.1. The Spherical Coil with a Permeable Core
The spherical coil developed in Example 8.5.1 is now filled with
a uniform core having the permeability  . With the field
intensity again represented in terms of the magnetic scalar potential,
H = -
. With the field
intensity again represented in terms of the magnetic scalar potential,
H = -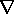 \Psi, the analysis differs only slightly from that
already carried out. Laplace's equation, (1), again prevails inside
and outside the coil. At the coil surface, the tangential H
again suffers a discontinuity equal to the surface current density in
accordance with Ampère's continuity condition, (4). The effect
of the permeable material is only felt through the flux continuity
condition, (3), which requires that
\Psi, the analysis differs only slightly from that
already carried out. Laplace's equation, (1), again prevails inside
and outside the coil. At the coil surface, the tangential H
again suffers a discontinuity equal to the surface current density in
accordance with Ampère's continuity condition, (4). The effect
of the permeable material is only felt through the flux continuity
condition, (3), which requires that

Thus, the normal flux continuity condition of (8.5.12) is
generalized to include the effect of the permeable material by

and it follows that the coefficients needed to evaluate \Psi, and
hence H, are now
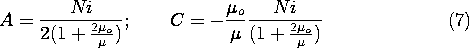
Substitution of these coefficients into (8.5.10) and (8.5.11)
gives the field inside and outside the spherical coil.
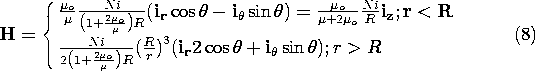
If the coil is highly permeable, these expressions show that
the field intensity inside is much less than that outside. In the
limit of "infinite permeability," where  o /
o /
 0, the field inside is zero while that outside becomes
0, the field inside is zero while that outside becomes

This is the surface current density, (8.5.6). A surface current
density backed by a highly permeable material terminates the
tangential magnetic field. Thus, Ampère's continuity condition
relating the fields to each side of the surface is replaced by a
boundary condition on the field on the low permeability side of the
interface. Using this boundary condition, that H a be equal
to the given K
a be equal
to the given K , (8.5.6), the solution for the exterior
\Psi and H can be written by inspection in the limit when
, (8.5.6), the solution for the exterior
\Psi and H can be written by inspection in the limit when


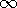 .
.
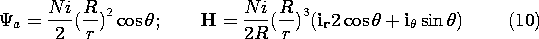
The interior magnetic flux density can in turn be
approximated by using this exterior field to compute the flux
density normal to the surface. Because this flux density must be the
same inside, finding the interior field reduces to solving Laplace's
equation for \Psi subject to the boundary condition that
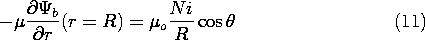
Again, the solution represents a uniform field and can be written by
inspection.

The H field, the gradient of the above expression, is indeed
that given by
(8a) in the limit where  o /
o / is small. Note that the
interior H goes to zero as the permeability goes to infinity,
but the interior flux density B remains finite. This fact
makes it clear that the inductance of the coil must remain finite,
even in the limit where
is small. Note that the
interior H goes to zero as the permeability goes to infinity,
but the interior flux density B remains finite. This fact
makes it clear that the inductance of the coil must remain finite,
even in the limit where 

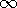 .
.
To determine an expression for the inductance that is valid
regardless of the core permeability, (8a) can be used to evaluate
(8.5.18). Note that the internal flux density B that replaces
 o Hz is 3
o Hz is 3 /[
/[ + 2
+ 2 o] times larger than the
flux density in the absence of the magnetic material. This
enhancement factor increases monotonically with the ratio
o] times larger than the
flux density in the absence of the magnetic material. This
enhancement factor increases monotonically with the ratio
 /
/ o but reaches a maximum of only 3 in the limit where
this ratio goes to infinity. Once again, we have evidence of the
core demagnetization caused by the surface magnetic charge induced
on the surface of the sphere.
o but reaches a maximum of only 3 in the limit where
this ratio goes to infinity. Once again, we have evidence of the
core demagnetization caused by the surface magnetic charge induced
on the surface of the sphere.
With the uniformity of the field inside the sphere known in
advance, a much simpler derivation of (8a) gives further insight into
the role of the magnetization. Thus, in the core, the H-field is the
superposition of two fields. The first is caused by the surface
current, and given by (8a) with  =
=  o.
o.

The second is due to the uniform magnetization M = Miz,
which is given by the magnetization analog to (6.3.15) (E
 H , P \rightarrow
H , P \rightarrow  o M ,
o M ,  o
o

 o ).
o ).

The net internal magnetic field intensity is the sum of these.

Only now do we introduce the constitutive law relating Mo to Hz,
Mo = 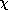 m Hz. [In Sec. 9.8 we will exploit the fact that the
relation could be nonlinear.] If this law is introduced into (15),
and that expression solved for Hz, a result is obtained that is
familiar from from (8a).
m Hz. [In Sec. 9.8 we will exploit the fact that the
relation could be nonlinear.] If this law is introduced into (15),
and that expression solved for Hz, a result is obtained that is
familiar from from (8a).
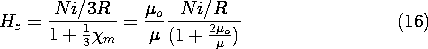
This last calculation again demonstrates how the field Ni/3R is
reduced by the magnetization through the "feedback factor"
1/[1 + (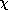 m /3)].
m /3)].
Magnetic circuit models, introduced in the next section, exploit
the capacity of highly permeable materials to guide the magnetic flux.
The example considered next uses familiar solutions to Laplace's
equation to illustrate how this guiding takes place. We will make
reference to this case study when the subject of magnetic circuits is
initiated.
Example 9.6.2. Field Model for a Magnetic Circuit
A small coil with N turns and excited by a current i
is used to make a magnetic
field in a spherically shaped material of permeability  b. As shown
in Fig. 9.6.1, the coil has radius R, while the
b. As shown
in Fig. 9.6.1, the coil has radius R, while the  sphere has radius
b and is surrounded by a magnetic medium of permeability
sphere has radius
b and is surrounded by a magnetic medium of permeability  a.
a.

Because the coil radius is small compared to that of the sphere,
it will be modeled as a dipole having its moment m =  R2 i in
the z direction. It follows from (8.3.13) that the magnetic scalar
potential for this dipole is
R2 i in
the z direction. It follows from (8.3.13) that the magnetic scalar
potential for this dipole is

No surface current density exists at the surface of the sphere.
Thus, Ampère's continuity law requires that
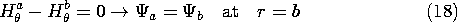
Also, at the interface, the flux continuity condition is
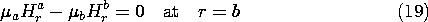
Finally, the only excitation of the field is the coil at the origin,
so we require that the field decay to zero far from the sphere.

Given that the scalar potential has the  dependence
cos (
dependence
cos ( ), we look for solutions
having this same
), we look for solutions
having this same  dependence. In the exterior region, the
solution representing a uniform field is ruled out because there is no
field at infinity. In the neighborhood of the origin, we know that
\Psi must approach the dipole field. These two conditions are
implicit in the assumed solutions
dependence. In the exterior region, the
solution representing a uniform field is ruled out because there is no
field at infinity. In the neighborhood of the origin, we know that
\Psi must approach the dipole field. These two conditions are
implicit in the assumed solutions
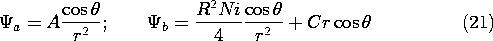
while the coefficients A and C are available to satisfy the two
remaining continuity conditions, (18) and (19). Substitution gives
two expressions which are linear in A and C and which can be
solved to give
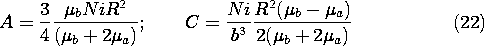
We thus conclude that the scalar magnetic potential outside the sphere
is that of a dipole
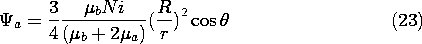
while inside it is that of a dipole plus that of a uniform field.
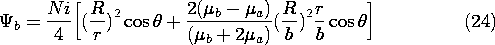
For increasing values of the relative permeability, the
equipotentials and field lines are shown in Fig. 9.6.2. With
 b/
b/ a = 1, the field is simply that of the dipole at the
origin. In the opposite extreme, where the ratio of permeabilities is
100, it has become clear that the interior field lines tend to
become tangential to the spherical surface.
a = 1, the field is simply that of the dipole at the
origin. In the opposite extreme, where the ratio of permeabilities is
100, it has become clear that the interior field lines tend to
become tangential to the spherical surface.

The results of Fig. 9.6.2 can be elaborated by taking the limit of
 b /
b / a going to infinity. In this limit, the scalar
potentials are
a going to infinity. In this limit, the scalar
potentials are

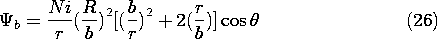
In the limit of a large permeability of the medium in which the coil
is imbedded relative to that of the surrounding medium, guidance of
the magnetic flux occurs by the highly permeable medium. Indeed,
in this limit, the flux produced by the coil goes to infinity,
whereas the flux of the field \int H  da escaping from
the sphere (the so-called "fringing") stays finite, because the
exterior potential stays finite. The magnetic
flux \int B
da escaping from
the sphere (the so-called "fringing") stays finite, because the
exterior potential stays finite. The magnetic
flux \int B  da is guided within the sphere, and
practically no magnetic flux escapes. The flux lines on the inside
surface of
the highly permeable sphere can be practically tangential as indeed
predicted by (26).
da is guided within the sphere, and
practically no magnetic flux escapes. The flux lines on the inside
surface of
the highly permeable sphere can be practically tangential as indeed
predicted by (26).
Another limit of interest is when the outside medium is highly
permeable and the coil is situated in a medium of low permeability
(like free space). In this limit, one obtains

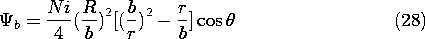
The surface at r = b becomes an equipotential of \Psi. The
magnetic field is perpendicular to the surface. The highly permeable
medium behaves in a way analogous to a perfect conductor in the
electroquasistatic case.
In order to gain physical insight,
two types of approximate boundary conditions have been illustrated in
the previous example. These apply when one region is of much greater
permeability than another. In the limit of infinite permeability
of one of the regions, the two continuity conditions at the interface
between these regions reduce to one boundary condition on the fields
in one of the regions. We conclude this section with a summary of
these boundary conditions.

At a boundary between regions (a) and (b), having
permeabilities  a and
a and  b, respectively, the normal flux density
b, respectively, the normal flux density
 Hn is continuous. If there is no surface current density,
the tangential components Ht are also continuous. Thus, the
magnetic field intensity to either side of the interface is as shown
in Fig. 9.6.3. With the angles between H and the normal on each
side of the interface denoted by
Hn is continuous. If there is no surface current density,
the tangential components Ht are also continuous. Thus, the
magnetic field intensity to either side of the interface is as shown
in Fig. 9.6.3. With the angles between H and the normal on each
side of the interface denoted by  and
and  , respectively,
, respectively,
The continuity conditions can be used to express \tan ( ) in
terms of the fields on the (b) side of the interface, so it follows that
) in
terms of the fields on the (b) side of the interface, so it follows that

In the limit where  a /
a / b
b  0, there are therefore
two possibilities. Either \tan (
0, there are therefore
two possibilities. Either \tan ( )
)  0, so that
0, so that

 0 and H in region (a) becomes
perpendicular to the boundary, or \tan (
0 and H in region (a) becomes
perpendicular to the boundary, or \tan ( )
) 
 so that
so that 
 90 degrees and H in region (b)
becomes tangential to the boundary. Which of these two possibilities
pertains depends on the excitation configuration.
90 degrees and H in region (b)
becomes tangential to the boundary. Which of these two possibilities
pertains depends on the excitation configuration.
Excitation in Region of High Permeability
In these configurations,
a closed contour can be found within the highly permeable material
that encircles current-carrying wires. For the coil at the center of the
highly permeable sphere considered in Example 9.6.2, such a contour
is as shown in Fig. 9.6.4. As  b
b 
 , the flux density
B also goes to infinity. In this limit, the flux escaping from the
body can be ignored compared to that guided by the body. The boundary
is therefore one at which the interior flux density is essentially
tangential.
, the flux density
B also goes to infinity. In this limit, the flux escaping from the
body can be ignored compared to that guided by the body. The boundary
is therefore one at which the interior flux density is essentially
tangential.

Once the field has been determined in the infinitely permeable
material, continuity of tangential H is used to provide a boundary
condition on the free space side of the interface.

Excitation in Region of Low Permeability
In this second class of configurations, there is no closed contour
within the highly permeable material that encircles a
current-carrying wire. If the current-carrying wires are within the
free space region, as in Fig. 9.6.5a, a contour must leave the highly
permeable material to encircle the wire. In the limit where
 b
b 
 , the magnetic field intensity in the
highly permeable material approaches zero, and thus H on the
interior side of the interface becomes perpendicular to the boundary.
, the magnetic field intensity in the
highly permeable material approaches zero, and thus H on the
interior side of the interface becomes perpendicular to the boundary.


With wires on the interface between regions comprising a surface
current density, as illustrated in Fig. 9.6.5b, it is still not
possible to encircle the current without following a contour that
leaves the highly permeable material. Thus, the case of a surface
current is also in this second category. The tangential H is
terminated by the surface current density. Thus, the boundary
condition on H on the interior side of the interface carrying the
surface current K is

This boundary condition was illustrated in Example 9.6.1.
Once the fields in the interior region have been found,
continuity of normal flux density provides a boundary condition for
determining the flux distribution in the highly permeable region.
9.7 Magnetic Circuits
The availability of relatively inexpensive magnetic materials,
with magnetic susceptibilities of the order of 1000 or more, allows
the production of high magnetic flux densities with relatively small
currents. Devices designed to exploit these materials include
compact inductors, transformers, and rotating machines. Many of these
are modeled as the magnetic circuits that are the theme of this
section.

A magnetic circuit typical of transformer cores is shown
in Fig. 9.7.1. A core of high permeability material has a pair of
rectangular windows cut through its center. Wires passing through
these windows are wrapped around the central column. The flux
generated by this coil tends to be guided by the magnetizable
material. It passes upward through the center leg of the material, and
splits into parts that circulate through the legs to left and right.
Example 9.6.2, with its highly permeable sphere excited by a small
coil, offered the opportunity to study the trapping of magnetic
flux. Here, as in that case with  b /
b / a \gg 1,
the flux density inside the core tends to be tangential
to the surface. Thus, the magnetic flux density is guided by the
material and the field distribution within the core tends to be
independent of the exterior configuration.
a \gg 1,
the flux density inside the core tends to be tangential
to the surface. Thus, the magnetic flux density is guided by the
material and the field distribution within the core tends to be
independent of the exterior configuration.
In situations of this type, where the ducting of the magnetic
flux makes it possible to approximate the distribution of magnetic
field, the MQS integral laws serve much the same purpose as do
Kirchhoff's laws for electrical circuits.

The MQS form of Ampère's integral law applies to a contour, such
as C1 in Fig. 9.7.2, following a path of circulating magnetic
flux.

The surface enclosed by this contour in Fig. 9.7.2 is pierced N times
by the current carried by the wire, so the surface integral of the
current density on the right in (1) is, in this case, Ni. The same
equation could be written for a contour circulating through the left
leg, or for one circulating around through the outer legs. Note that
the latter would enclose a surface S through which the net current
would be zero.
If Ampère's integral law plays a role analogous to Kirchhoff's
voltage law, then the integral law expressing continuity of magnetic
flux is analogous to Kirchhoff's current law. It requires that
through a closed surface, such as S2 in Fig. 9.7.2, the net
magnetic flux is zero.

As a result, the flux entering
the closed surface S2 in Fig. 9.7.2 through the central leg must
be equal to that leaving to left and right through the upper legs of
the magnetic circuit. We will return to this particular magnetic
circuit when we discuss transformers.
Example 9.7.1. The Air Gap Field of an Electromagnet
The magnetic circuit of Fig. 9.7.3 might be used to produce a
high magnetic field intensity in the narrow air gap. An N-turn coil
is wrapped around the left leg of the highly permeable core. Provided
that the length g of the air gap is not too large, the flux
resulting from the current i in this winding is largely guided along
the magnetizable material.

By approximating the fields in sections of the circuit as being
essentially uniform, it is possible to use the integral laws to
determine the field intensity in the gap. In the left leg, the field
is approximated by the constant H1 over the length l1 and
cross-sectional area A1. Similarly, over the lengths l2,
which have the cross-sectional areas A2, the field intensity is
approximated by H2. Finally, under the assumption that the gap
width g is small compared to the cross-sectional dimensions of the
gap, the field in the gap is represented by the constant Hg. The
line integral of H in Ampère's integral law, (1), is then applied
to the contour C that follows the magnetic field intensity around the
circuit to obtain the left-hand side of the expression
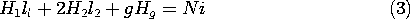
The right-hand side of this equation represents the surface integral
of J  d a for a surface S having this contour as its edge.
The total current through the surface is simply the current through
one wire multiplied by the number of times it pierces the surface
S.
d a for a surface S having this contour as its edge.
The total current through the surface is simply the current through
one wire multiplied by the number of times it pierces the surface
S.
We presume that the magnetizable material is operated under
conditions of magnetic linearity. The constitutive law then relates
the flux density and field intensity in each of the regions.
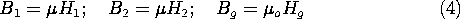
Continuity of magnetic flux, (2), requires that the total flux
through each section of the circuit be the same. With the flux
densities expressed using (4), this requires that
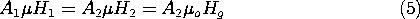
Our objective is to determine Hg. To that end, (5) is used
to write
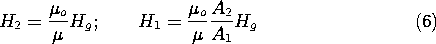
and these relations used to eliminate H1 and H2 in favor of
Hg in (3). From the resulting expression, it follows that
Note that in the limit of infinite core permeability, the gap
field intensity is simply Ni/g.
If the magnetic circuit can be broken into sections in which the
field intensity is essentially uniform, then the fields may be
determined from the integral laws. The previous example
is a case in point. A more general approach is required if the core
is of complex geometry or if a more accurate model is required.
We presume throughout this chapter that the magnetizable material
is sufficiently insulating so that even if the fields are time varying,
there is no current density in the core. As a result, the magnetic
field intensity in the core can be represented in terms of the scalar
magnetic potential introduced in Sec. 8.3.

According to Ampère's integral law, (1), integration of
H  ds around a closed contour must be equal to the
"Ampère turns" Ni passing through the surface spanning the
contour. With H expressed in terms of \Psi, integration from
(a) to (b) around a contour such as C in Fig. 9.7.4, which
encircles a net current equal
to the product of the turns N and the current per turn i, gives
\Psia - \Psib \equiv
ds around a closed contour must be equal to the
"Ampère turns" Ni passing through the surface spanning the
contour. With H expressed in terms of \Psi, integration from
(a) to (b) around a contour such as C in Fig. 9.7.4, which
encircles a net current equal
to the product of the turns N and the current per turn i, gives
\Psia - \Psib \equiv  \Psi = Ni. With (a) and (b) adjacent
to each other, it is clear that \Psi is multiple-valued. To specify the
principal value of this multiple-valued function we must introduce a
discontinuity in \Psi somewhere along the contour. In the circuit of
Fig. 9.7.4, this discontinuity is defined to occur across the surface
Sd.
\Psi = Ni. With (a) and (b) adjacent
to each other, it is clear that \Psi is multiple-valued. To specify the
principal value of this multiple-valued function we must introduce a
discontinuity in \Psi somewhere along the contour. In the circuit of
Fig. 9.7.4, this discontinuity is defined to occur across the surface
Sd.

To make the line integral of H  ds from any point
just above the surface Sd around the circuit to a point just below
the surface equal to Ni, the potential is required to suffer a
discontinuity
ds from any point
just above the surface Sd around the circuit to a point just below
the surface equal to Ni, the potential is required to suffer a
discontinuity  \Psi = Ni across Sd. Everywhere inside the
magnetic material, \Psi satisfies Laplace's equation. If, in
addition,
the normal flux density on the walls of the magnetizable material is
required to vanish, the distribution of \Psi within the core is
uniquely determined. Note that only the discontinuity in \Psi is
specified on the surface Sd. The magnitude of \Psi on one side
or the other is not specified. Also, the normal derivative of \Psi,
which is proportional to the normal component of H, must be
continuous across Sd.
\Psi = Ni across Sd. Everywhere inside the
magnetic material, \Psi satisfies Laplace's equation. If, in
addition,
the normal flux density on the walls of the magnetizable material is
required to vanish, the distribution of \Psi within the core is
uniquely determined. Note that only the discontinuity in \Psi is
specified on the surface Sd. The magnitude of \Psi on one side
or the other is not specified. Also, the normal derivative of \Psi,
which is proportional to the normal component of H, must be
continuous across Sd.
The following simple example shows how the scalar magnetic
potential can be used to determine the field inside a magnetic
circuit.
Example 9.7.2. The Magnetic Potential inside a Magnetizable Core
The core of the magnetic circuit shown in Fig. 9.7.5 has outer and
inner radii a and b, respectively, and a length d in the z
direction that is large compared to a. A current i is carried in
the z direction through the center hole and returned on the outer
periphery by N turns. Thus, the integral of H  ds
over a contour
circulating around the magnetic circuit must be Ni, and a surface of
discontinuity Sd is arbitrarily introduced as shown in Fig.
9.7.5. With the boundary condition of no flux leakage,
ds
over a contour
circulating around the magnetic circuit must be Ni, and a surface of
discontinuity Sd is arbitrarily introduced as shown in Fig.
9.7.5. With the boundary condition of no flux leakage,
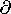 \Psi /\partial r = 0 at r = a and at r = b, the
solution to Laplace's equation within the core is uniquely specified.
\Psi /\partial r = 0 at r = a and at r = b, the
solution to Laplace's equation within the core is uniquely specified.

In principle, the boundary value problem can be solved even if
the geometry is complicated. For the configuration shown in Fig.
9.7.5, the requirement of no radial derivative suggests that \Psi is
independent of r. Thus, with A an arbitrary coefficient, a reasonable
guess is

The coefficient A has been selected so that there is indeed a
discontinuity Ni in \Psi between  = 2
= 2 and
and  = 0.
= 0.
The magnetic field intensity given by substituting (9) into (8) is

Note that H is continuous, as it should be.
Now that the inside field has been determined, it is possible,
in turn, to find the fields in the surrounding free space regions. The
solution for the inside field, together with the given surface
current distribution at the boundary between regions, provides the
tangential field at the boundaries of the outside regions. Within an
arbitrary constant, a boundary condition on \Psi is therefore
specified. In the outside regions, there is no closed contour that
both stays within the region and encircles current. In these regions,
\Psi is continuous. Thus, the problem of finding the "leakage" fields
is reduced to finding the boundary value solution to Laplace's equation.
This inside-outside approach gives an approximate field
distribution that is justified only if the relative permeability of
the core is very large. Once the outside field is approximated in
this way, it can be used to predict how much flux has left the
magnetic circuit and hence how much error there is in the calculation.
Generally, the error will be found to depend not only on the relative
permeability but also on the geometry. If the magnetic circuit is
composed of legs that are long and thin, then we would expect the
leakage of flux to be large and the approximation of the
inside-outside approach to become invalid.
Electrical Terminal Relations and Characteristics
Practical inductors (chokes) often take the form of magnetic circuits.
With more than one winding on the same magnetic circuit, the magnetic
circuit serves as the core of a transformer. Figure 9.7.6 gives the
schematic representation of a transformer. Each winding is modeled
as perfectly conducting, so its terminal voltage is given by (9.2.12).

However, the flux linked by one winding is due to two currents. If
the core is magnetically linear, we have a flux linked by the first
coil that is the sum of a flux linkage L11 i1 due to its own
current and a flux linkage L12 due to the current in the second
winding. The situation for the second coil is similar. Thus, the
flux linkages are related to the terminal currents by an
inductance matrix.

The coefficients Lij are functions of the core and coil geometries
and properties of the material, with L11 and L22 the familiar
self-inductances and L12 and L21 the mutual
inductances.

The word "transformer" is commonly used in two ways, each often
represented schematically, as in Fig. 9.7.6. In the first, the
implication is only that the terminal relations are as summarized by
(12). In the second usage, where the device is said to be an ideal
transformer, the terminal relations are given as voltage and
current ratios. For an ideal transformer,
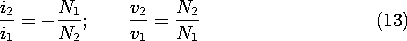
Presumably, such a device can serve to step up the voltage while
stepping down the current. The relationships between terminal
voltages and between terminal currents is linear, so that such a
device is "ideal" for processing signals.
The magnetic circuit developed in the next example is that of a
typical transformer. We have two objectives. First, we determine the
inductances needed to complete (12). Second, we define the
conditions under which such a transformer operates as an ideal
transformer.
Example 9.7.3. A Transformer
The core shown in Fig. 9.7.7 is familiar from the introduction to
this section, Fig. 9.7.1. The "windows" have been filled up by a
pair of windings, having the turns N1 and N2, respectively.
They share the center leg of the magnetic circuit as a common core and
generate a flux that circulates through the branches to either side.

The relation between the terminal voltages for an ideal transformer
depends only on unity coupling between the two windings. That is, if
we call 
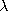 the magnetic flux through the center leg, the
flux linking the respective coils is
the magnetic flux through the center leg, the
flux linking the respective coils is
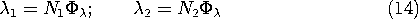
These statements presume that there is no leakage flux which would
link one coil but bypass the other.
In terms of the magnetic flux through the center leg, the
terminal voltages follow from (14) as
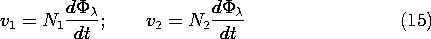
From these expressions, without further restrictions on
the mode of operation, follows the relation between the terminal
voltages of (13).
We now use the integral laws to determine the flux linkages in
terms of the currents. Because it is desirable to minimize the peak
magnetic flux density at each point throughout the core, and because
the flux through the center leg divides evenly between the two
circuits, the cross-sectional areas of the return legs are made half
as large as that of the center leg.
3 To optimize the usage
of core material, the relative dimensions are often taken as in the
inset to Fig. 9.7.7. Two cores are cut from rectangular sections
measuring 6h x 8h. Once the windows have been removed, the
rectangle is cut in two, forming two "E" cores which can then be
combined with the "I's" to form two complete cores. To reduce
eddy currents, the core is often made from varnished laminations.
This will be discussed in Chap. 10. As a result, the magnitude of
B, and hence H, can be approximated as constant throughout
the core. [Note that we have now used the flux continuity condition
of (2).]
With the average length of a circulating magnetic field line
taken as l, Ampère's integral law, (1), gives

In view of the presumed magnetic linearity of the core, the flux
through the cross-sectional area A of the center leg is

and it follows from these last two expressions that
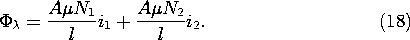
Multiplication by the turns N1 and then N2, respectively, gives
the flux linkages 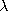 1 and
1 and 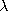 2.
2.
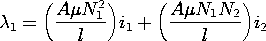
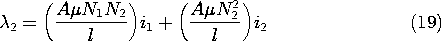
Comparison of this expression with (12) identifies the self- and mutual
inductances as
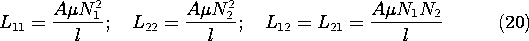
Note that the mutual inductances are equal. In Sec. 11.7, we shall see
that this is a consequence of energy conservation. Also, the
self-inductances are related to either mutual inductance by

Under what conditions do the terminal currents obey the relations for
an "ideal transformer"?
Suppose that the (1) terminals are selected as the "primary"
terminals of the transformer and driven by a current source I(t), and
that the terminals of the (2) winding, the "secondary," are connected
to a resistive load R. To recognize that the winding in fact has an
internal resistance, this load includes the winding resistance as
well. The electrical circuit is as shown in Fig. 9.7.8.

The secondary circuit equation is

and using (12) with i1 = I, it follows that the secondary current
i2 is governed by
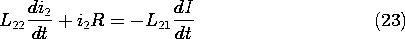
For purposes of illustration, consider the response to a drive that is
in the sinusoidal steady state. With the drive angular frequency
equal to  , the response has the same time dependence in the
steady state.
, the response has the same time dependence in the
steady state.
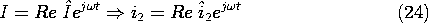
Substitution into (23) then shows that the complex amplitude of the
response is
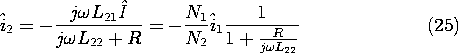
The ideal transformer-current relation is obtained if

In that case, (25) reduces to

When the ideal transformer condition, (26), holds, the first term on
the left in (23) overwhelms the second. What remains if the
resistance term is neglected is the statement
We conclude that for ideal transformer operation, the flux
linkages are negligible. This is crucial to having a transformer
behave as a linear device. Whether represented by the inductance
matrix of (12) or by the ideal relations of (13), linear operation
hinges on having a linear relation between B and H in the core,
(17). By operating in the regime of (26) so that B is small enough
to avoid saturation, (17) tends to remain valid.
9.8 Summary
The magnetization density M represents the density of
magnetic dipoles. The moment m of a single microscopic magnetic
dipole was defined in Sec. 8.2. With  o m \leftrightarrow
p where
p is the moment of an electric dipole, the magnetic and electric
dipoles play analogous roles, and so do the H and E fields. In
Sec. 9.1, it was therefore natural to define the magnetization density
so that it played a role analogous to the polarization density,
o m \leftrightarrow
p where
p is the moment of an electric dipole, the magnetic and electric
dipoles play analogous roles, and so do the H and E fields. In
Sec. 9.1, it was therefore natural to define the magnetization density
so that it played a role analogous to the polarization density,
 o M \leftrightarrow P. As a result, the magnetic charge
density
o M \leftrightarrow P. As a result, the magnetic charge
density  m was considered to be a source of
m was considered to be a source of 

 o
H. The relations of these sources to the magnetization density
are the first expressions summarized in Table 9.8.1.
The second set of relations are different forms of the flux
continuity law, including the effect of magnetization. If the
magnetization density is given, (9.2.2) and (9.2.3) are most useful.
However, if M is induced by H, then it is convenient to
introduce the magnetic flux density B as a variable. The
correspondence between the fields due to magnetization and those due
to polarization is B \leftrightarrow D.
o
H. The relations of these sources to the magnetization density
are the first expressions summarized in Table 9.8.1.
The second set of relations are different forms of the flux
continuity law, including the effect of magnetization. If the
magnetization density is given, (9.2.2) and (9.2.3) are most useful.
However, if M is induced by H, then it is convenient to
introduce the magnetic flux density B as a variable. The
correspondence between the fields due to magnetization and those due
to polarization is B \leftrightarrow D.

The third set of relations pertains to linearly
magnetizable materials. There is no magnetic analog to the
unpaired electric charge density.
In this chapter, the MQS form of Ampère's law was also required to
determine H.

In regions where J=0, H is indeed analogous to E in
the polarized EQS systems of Chap. 6. In any case, if J is given,
or if it is on perfectly conducting surfaces, its contribution to the
magnetic field intensity is determined as in Chap. 8.
In Chap. 10, we introduce the additional laws required to
determine J self-consistently in materials of finite conductivity.
To do this, it is necessary to give careful attention to the electric
field associated with MQS fields. In this chapter, we have generalized
Faraday's law, (9.2.11),

so that it can be used to determine E
in the presence of magnetizable materials. Chapter 10 brings this law
to the fore as it plays a key role in determining the self-consistent
J.

 \hbar is Planck's constant, \hbar =
1.05 x 10-34 joule-sec so that me has the units A -
m2. The quantum mechanics of atoms and molecules dictates that,
whether due to the orbits or to the spins, the electronic
contributions to their net dipole moments tend to cancel.
Those that do make a contribution are typically in unfilled shells.
\hbar is Planck's constant, \hbar =
1.05 x 10-34 joule-sec so that me has the units A -
m2. The quantum mechanics of atoms and molecules dictates that,
whether due to the orbits or to the spins, the electronic
contributions to their net dipole moments tend to cancel.
Those that do make a contribution are typically in unfilled shells.
 (kg/m3).
Thus, for a sphere having radius R, the sum of the dipole moments is
(kg/m3).
Thus, for a sphere having radius R, the sum of the dipole moments is

 R2, is set
equal to that of the sphere, (2), it follows that i must be
R2, is set
equal to that of the sphere, (2), it follows that i must be

 = 7.86 x 103 and Mo = 56) and a
radius of 10 cm, the current required to produce the same magnetic
moment is 105 A.
= 7.86 x 103 and Mo = 56) and a
radius of 10 cm, the current required to produce the same magnetic
moment is 105 A.
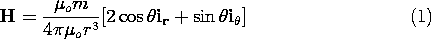
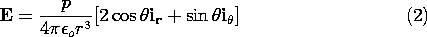


 o m, the
analog of the polarization density P is
o m, the
analog of the polarization density P is 

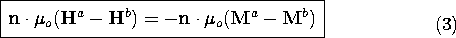
 sm.
sm.

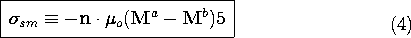
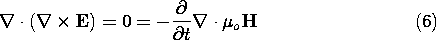
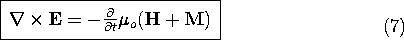







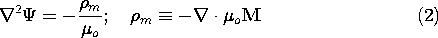
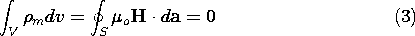

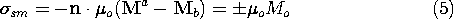

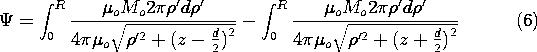
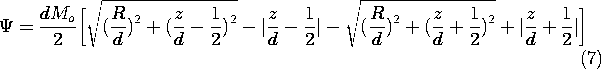
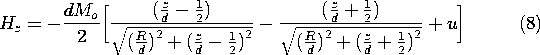


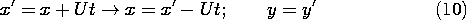
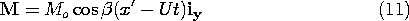
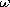 =
=  U. This relationship
between the fixed frame frequency and the spatial periodicity
suggests how the distribution of magnetization is established by "recording"
a signal having the frequency
U. This relationship
between the fixed frame frequency and the spatial periodicity
suggests how the distribution of magnetization is established by "recording"
a signal having the frequency 

 \pm
\pm  .
.
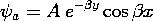

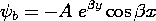
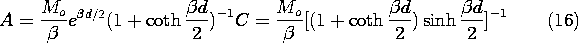
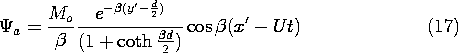
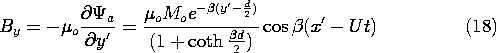
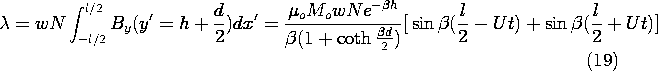
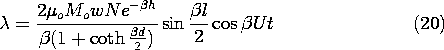
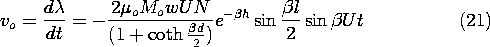




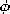 directed. The integral MQS form of Ampère's law is written for a
contour C circulating about the toroidal axis within the core and at a
radius r. Because the major radius R of the torus is large compared
to the minor radius
directed. The integral MQS form of Ampère's law is written for a
contour C circulating about the toroidal axis within the core and at a
radius r. Because the major radius R of the torus is large compared
to the minor radius  w, we will ignore the variation of
r over the cross-section of the torus and approximate r by an
average radius R. The surface S spanned by this contour and shown
in Fig. 9.4.2 is pierced N1 times by the current i, giving a total
current of N1 i. Thus, the azimuthal field inside the core is
essentially
w, we will ignore the variation of
r over the cross-section of the torus and approximate r by an
average radius R. The surface S spanned by this contour and shown
in Fig. 9.4.2 is pierced N1 times by the current i, giving a total
current of N1 i. Thus, the azimuthal field inside the core is
essentially



 , and hence through (2),
to B.
, and hence through (2),
to B.

 m is the magnetic susceptibility. More commonly,
the constitutive law for a magnetically linear material is written in
terms of the magnetic flux density, defined by (9.2.8).
m is the magnetic susceptibility. More commonly,
the constitutive law for a magnetically linear material is written in
terms of the magnetic flux density, defined by (9.2.8).
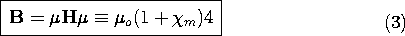







 \Psi,
or we can follow the lead from Sec. 8.6 and use the vector potential
to represent the flux density by letting B =
\Psi,
or we can follow the lead from Sec. 8.6 and use the vector potential
to represent the flux density by letting B = 






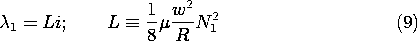



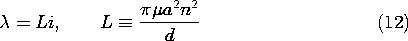

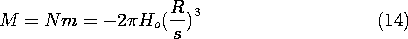

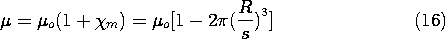



 L.
L.
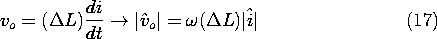
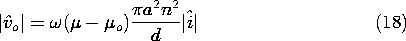
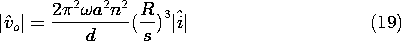

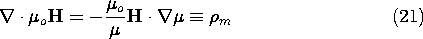
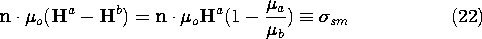
 are taken by H,
B, and
are taken by H,
B, and 
 A) -
A) - 




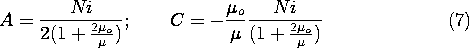
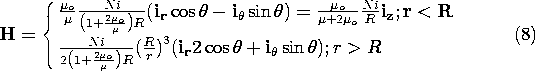

 a be equal
to the given K
a be equal
to the given K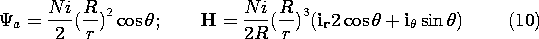
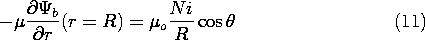




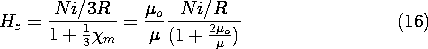


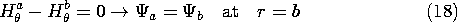
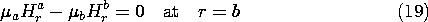

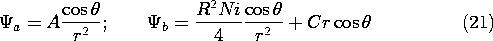
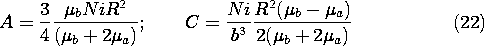
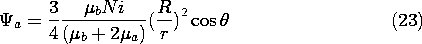
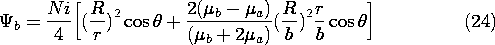


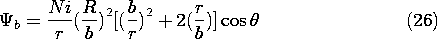

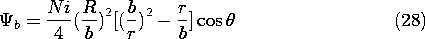

 and
and 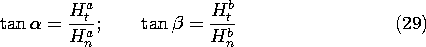











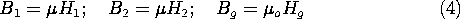
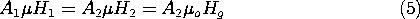
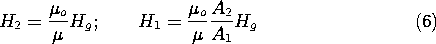
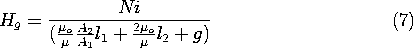


 \Psi /\partial r = 0 at r = a and at r = b, the
solution to Laplace's equation within the core is uniquely specified.
\Psi /\partial r = 0 at r = a and at r = b, the
solution to Laplace's equation within the core is uniquely specified.