Problem 1. A 3:1 multiplexer has the following inputs and output:

The value of output Y is determined as follows:

Write a Verilog module for the 3:1 multiplexer that implements the sum-of-products equation for Y:
```
    __ __         __     
Y = S0*S1*D0 + S0*S1*D1 + S1*D2
```
Use a dataflow style for your code (ie, use "assign" to set the values of your signals).

Write a Verilog module for the 3:1 multiplexer that uses the "?" operator. Again use a dataflow style for your code (ie, use "assign" to set the values of your signals).

Write a Verilog module for the 3:1 multiplexer that uses the "case" statement. Remember that a "case" statement can only appear inside of a behavioral block.

Problem 2. When creating a behavioral block using Verilog's ALWAYS statement, one supplies a sensitivity list -- a list of signals that trigger execution of the block when they change value. For example, here's full adder module which uses an ALWAYS block:

module fulladder(a,b,cin,sum,cout);
  input a,b,cin;
  output sum,cout;

  reg sum,cout;
  always @ (a or b or cin)
  begin
    sum <= a ^ b ^ cin;
    cout <= (a & b) | (a & cin) | (b & cin);
  end
endmodule

When writing behavioral implementations of combinational logic all the signals appearing on the right-hand side of assignment statements (ie, signals whose values are used in computations) should appear in the sensitivity list.

What would be the effect of, say, omitting cin from the sensitivity list above?

Problem 3. Using the Verilog parameter mechanism it's possible to write modules whose operation depends on parameters specified when the module is instantiated.

Write a parameterized parity module that takes as input a vector whose size is set by the parameter. The module has a single output which is 1 if the number of 1's in the input vector is odd and 0 otherwise.

How would one instantiate an instance of your module to compute parity on the 16-bit wide data bus DATA[15:0]?

Problem 4. Consider the following combinational circuit that adds to 8-bit numbers. The circuit includes carry-in (CIN) and carry-out (COUT) signals so that it can be cascaded to form wider adders.

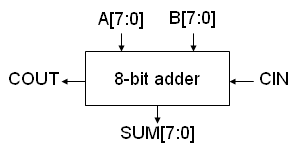
Where possible, it's best to use the built-in Verilog operators for integer arithmetic. This makes it easy for the CAD tools to map your logic onto the special-purpose arithmetic circuitry provided by many of today's FPGAs. Write a Verilog module for the 8-bit adder that uses the Verilog "+" operator. Use a dataflow style for your code (ie, use "assign" to set the values of your signals).

A common method for building fast adders is to rewrite the equations for SUM and COUT in terms of P (propagate) and G (generate) signals. P is true if a carry-in will be propagated to the carry-out; G is true if a carry-out will be generated regardless of the value of the carry-in.
The advantage of this formulation is that P and G can be computed in parallel for all the bits of the adder since they don't depend on CIN. This will shorten the delay between CIN and COUT.
Write a Verilog module for the 8-bit adder that uses the P and G to compute SUM and COUT. Again use a dataflow style for your code.

It can be hard to see how the carry chain is working in the previous example. Sometimes it's easier to express what you want if you use a loop and compute the answer bit-by-bit. Write a Verilog module for the 8-bit adder that uses P and G, but this time use a for-loop inside a behavioral block to compute SUM and COUT bit-by-bit.

In the adder implementations above the carry ripples up through the bits starting with the least significant bit. The total propagation delay (tPD) of the circuit is determined by the logic along the path between CIN and COUT (known as the carry chain). In a ripple carry adder tPD is proportional to the number of bits in the adder.

We can improve tPD by reworking the carry logic to use a "lookahead" strategy -- we'll use the P and G signals for individual nodes to compute P and G signals for pairs of nodes. We can apply this strategy again, computing P and G for groups of 4 nodes, and so on. We're building a tree of these lookahead modules; each node in the tree has the same logic. Once CIN for the adder is available it is fed to the top node of the lookahead tree, where it's combined with P and G of the children to produce carry-ins for the children nodes. This process continues until carry-in arrives at the leaf nodes where it can be used to compute SUM. For an N-bit adder, the depth of the lookahead tree is log2(N). It takes two traversals of the lookahead tree to (Ps and Gs up the tree, CINs down the tree) in order to finish the computation of SUM -- a tPD that's proportional to log2(N).

The following figure (from Hennessy and Patterson) shows what we have in mind.

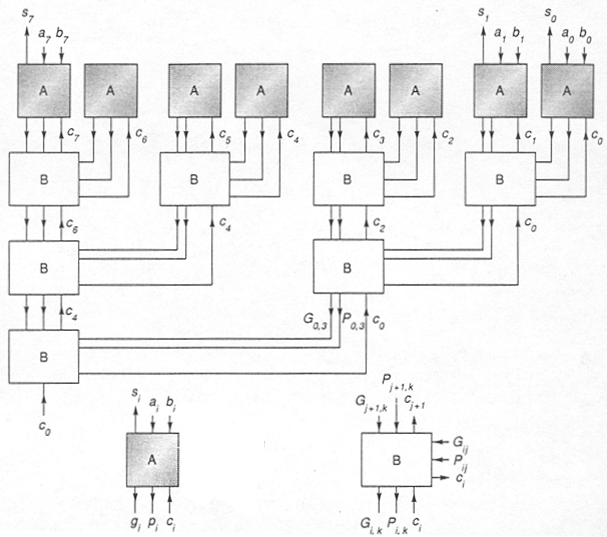
Here are the logic equations for the outputs of the A module in the figure above:
```
P = A ^ B
G = A * B
SUM = P ^ CIN
```
Write a Verilog implementation of the A module.

Here are the logic equations for the outputs of the B module in the figure above. P1 and G1 are the P and G signals from the right-hand connections to the B block; P2 and G2 from the top connections.
```
POUT = P1*P2
GOUT = G2 + P2*G1
C1 = CIN
C2 = G1 + P1*CIN
```
Write a Verilog implementation of the B module.

Using the A and B modules you created above, write a Verilog module for an 8-bit adder.

Verilog for Combinational Logic