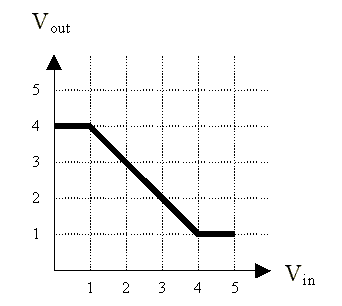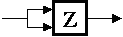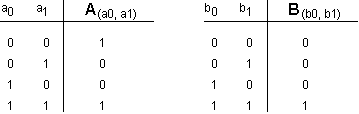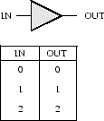
Problem 1. The behavior of a 1-input, 1-output device is measured by hooking a voltage source to its input and measuring the voltage at the output for several different input voltages:

We're interested in whether this device can serve as a legal combinational device that obeys the static discipline. For this device, obeying the static discipline means that

_IN

_IL

_OUT

_OH

_IN

_IH

_OUT

_OL

When answering the questions below, assume that all voltages are constrained to be in the range 0V to 5V.

Can one chose a V_OL of 0V for this device? Explain.

What's the smallest V_OL one can choose and still have the device obey the static discipline? Explain.

Assuming that we want to have 0.5V noise margins for both "0" and "1" values, what are appropriate voltage levels for V_OL, V_IL, V_IH, and V_OH so that the device obeys the static discipline. Hint: there are many possible choices, just choose one that obeys the constraints listed above.

Assuming that we want to have 0.5V noise margins for both "0" and "1" values, what is the largest possible voltage level for V_OL that still results in a device that obeys the static discipline?

Assuming that we want to have equal noise margins for both "0" and "1" values, what is the largest noise margin we can achieve with this device and still obey the static discipline?

Problem 2. Inverter madness.

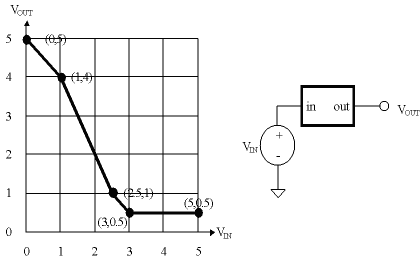
The following graph plots the voltage transfer characteristic for a device with one input and one output.
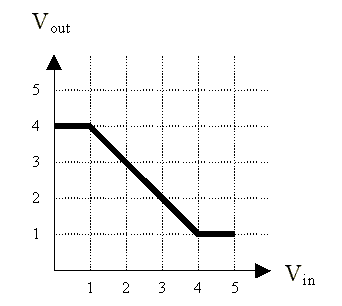Can this device be used as a combinational device in a logic family with 0.75V noise margins?

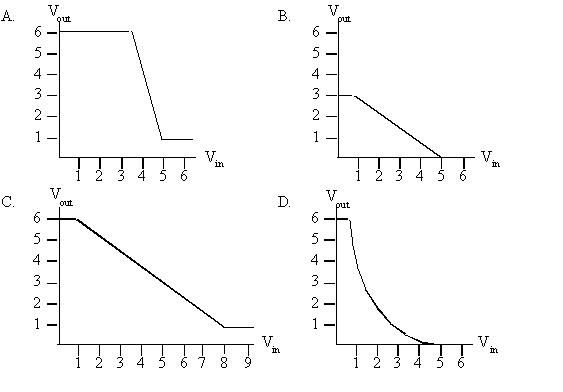
You are designing a new logic family and trying to decide on values of the four parameters V_IL, V_OL, V_IH, V_OH that lead to non-zero noise margins for various possible inverter designs. Four proposed inverter designs exhibit the voltage transfer characteristics shown in the diagrams below. For each design, either (1) specify suitable values of V_IL, V_OL, V_IH, V_OH. or (2) explain why no values for these parameters satisfy the static discipline.

Problem 3. Static discipline.

Consider a combinational buffer with one input and one output. Suppose we set its input to some voltage (V_IN), wait for the device to reach a steady state, then measure the voltage on its output (V_OUT) and find V_OUT < V_OL. What can we say about V_IN?

Now consider an inverter. Suppose we set its inputs to some voltage (V_IN), wait for the device to reach a steady state, then measure the voltage on its output (V_OUT) and find V_OUT > V_OH. What can we say about V_IN?

Problem 4. Ternary Logic.

Ternary is a term referring to the number system in base 3. Consider a convention in which a ternary digit is presented as an electric voltage between 0 and 10 V. Let 0-1 V represent a valid "0" output, 4-6 V a valid "1" output and 9-10 V a valid "2" output.

Assuming noise margins 1 V wide, show the mapping of logic levels to voltages for this ternary system. Include valid logic-level outputs, noise margins and forbidden zones. Your chart should resemble the following diagram, except of course it will incorporate 3 valid signal levels:

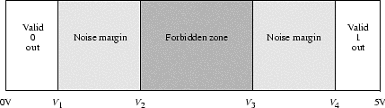
Graph the transfer characteristic for a device capable of acting as a ternary logic buffer, i.e., a device that produces at its output the same logic level present at its input, as shown below:

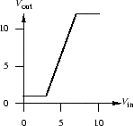
Can a device with the following transfer characteristic be used as a ternary logic buffer? Why or why not?

Problem 5. Bread and Circuits, Inc. has discovered an interesting electronic device (a Z-module) which is made using a single yeast cell, a speck of flour, and a grain of salt. The Z-module has two inputs carrying voltages VA and VB and a single output carrying VC. The output VC settles, after a 10ns period of stable input voltages, to the product of the input voltages restricted to range of 0V to 2V. In other words,

V_C =	V_A * V_B when 0 <= V_A * V_B <= 2
	2 when V_A * V_B > 2

Assume that the Z-module treats negative input voltages as if they were 0.

B&C is trying to make a logic family using Z-modules. As a starting point, they claim that

constitutes a valid combinational buffer under the proper voltage-to-logic representation conventions and will yield reasonable noise margins.

Which, if any, of the following proposed voltage thresholds yields a valid buffer with positive noise margins?

A. VOL = 1.5V  VIL = 1.6V  VIH = 1.7V  VOH = 1.8V
B. VOL = 0.7V  VIL = 0.9V  VIH = 1.1V  VOH = 1.3V
C. VOL = 0.1V  VIL = 0.3V  VIH = 1.7V  VOH = 1.9V
D. VOL = 0.5V  VIL = 0.5V  VIH = 1.5V  VOH = 1.5V

Determine the voltage thresholds that maximize the noise margins of B&C's buffer. If the noise margins are not independent, maximize the smaller of the two.

Ivan Idea, chief logician at B&C, is exploring the use of a single Z-module as a two-input logic gate, again with positive noise margins. He suspects that a Z-module, under the appropriate logic conventions, can be used for an AND or OR gate which obeys the static discipline. Ivan's been at it for several weeks and needs your help.
Can you find a way to use a Z-module for an AND or OR combinational device? If so, give the appropriate input and output voltage thresholds and the function performed. If not, carefully explain why the Z-module can't be used as AND or OR.

Ivan sidesteps the previous enigma by allowing himself the use of several Z-modules as components of a single logic gate. He assumes (and you may too) that noise enters the system only between logic gates, not between the components of a single gate. He notes that each of B&C's proposed buffers (using one Z-module) is an amplifier with gain greater than one. Ivan reasons that by cascading many such devices (as shown below), he can achieve arbitrarily high gain and hence excellent noise margins.

His plan is to use such a high-gain cascade on the output of a Z-module to restore the validity of marginal signal levels. Describe the voltage transfer characteristic (i.e, VIN vs. VOUT) of a cascade of a large number of Z-modules (via an expression or sketch).

Is there any way by which many Z-modules can be used to build a 2-input AND gate whose noise margins are both greater than 0.75V? If so, sketch an approach (giving a diagram and calculating the noise margins). If not, give a brief but convincing explanation.

Problem 6. Combinational construction rules

In lecture, we learned two basic principles regarding the class of combinational devices. The first allows us to build a combinational device from, e.g., electronic components:

A combinational device is a circuit element that has
- one or more digital inputs
- one or more digital outputs
- a functional specification that details the value of each output for every possible combination of valid input values
- a timing specification consisting (at minimum) of an upper bound t_pd on the required time for the device to compute the specified output values from an arbitrary set of stable, valid input values.

while the second allows us to construct complex combinational devices from acyclic circuits containing simpler ones:

A set of interconnected elements is a combinational device if
- each circuit element is combinational
- every input is connected to exactly one output or to some vast supply of 0's and 1's
- the circuit contains no directed cycles

In this problem, we ask you to think carefully about why these rules work - in particular, why an acyclic circuit of combinational devices, constructed according to the second principle, is itself a combinational device as defined by the first. You may assume for the following that every input and output is a logical 0 or 1.

Consider the following 2-input acyclic circuit whose two components, A and B, are each combinational devices:

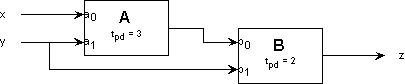
The propagation delay - the upper bound on the output settling time - for each device is specified in nanoseconds. The functional specifications for each component are given as truth tables detailing output values for each combination of inputs:

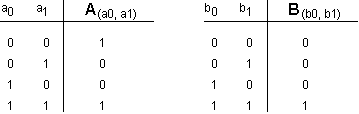
Give a truth table for the acyclic circuit, i.e. a table that specifies the value of z for each of the possible combinations of input values on x and y.

Describe a general procedure by which a truth table can be computed for each output of an arbitrary acyclic circuit containing only combinational components. [HINT: construct a functional specification to each circuit node].

Specify a propagation delay (the upper bound required for each combinational device) for the circuit.

Describe a general procedure by which a propagation delay can be computed for an arbitrary acyclic circuit containing only combinational components. [HINT: add a timing specification to each circuit node].

Do your general procedures for computing functional specifications and propagation delays work if the restriction to acyclic circuits is relaxed? Explain.

Problem 7. If you are given the following 2-input and 2-output combinational block:

with the following functional description: The output X is the the logical complement of the input A, and the output Y is the the logical complement of the input B. And valid ouputs are guaranteed after valid inputs have been established for 1 second.

Does this device adhere to the static disipline?

Suppose that the output X is connected to the input B, what output would you expect?

Suppose the functional description was changed to the following: The ouput X is a 1 if both A and B are "0", and Y is a 1 if either A or B but not both are "1". Does this change the answer the previous question?

The digital abstraction