Finite state machines

Problem 1. (Katz, problem 8.13) A finite state machine has one input and one output. The output becomes 1 and remains 1 thereafter when at least two 0's and two 1's have occurred as inputs, regardless of the order of appearance.

  1. Assuming this is to be implemented as a Moore machine, draw a state transition diagram for the machine. Hint: You can do this in nine states.
  1. Write a Verilog module that implements the machine. Your module should have the following inputs/outputs.

      CLK
        used to clock the FSM
      RESET
        asserted high to reset the FSM to its initial state
      ONE
        asserted high to input a "1". Note that this signal may stay high for many cycles (eg, it's generated by a button press) before returning low. Each high period should count as a single "1" input, ie, to inputs two "1"s in series, the signal must return low inbetween the first and second "1".
      ZERO
        asserted high to input a "0". This signal has the same timing protcol as ONE above.
      OUT
        asserted high when at least two "0"s and two "1"s have occurred as inputs.

    Assume that all inputs have been externally synchronized with clk.

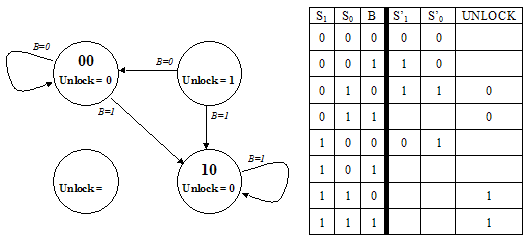
Problem 2. The ACME Company has recently received an order from a Mr. Wiley E. Coyote for their all-digital Perfectly Perplexing Padlock. The P3 has two buttons ("0" and "1") that when pressed cause the FSM controlling the lock to advance to a new state. In addition to advancing the FSM, each button press is encoded on the B signal (B=0 for button "0", B=1 for button "1"). The padlock unlocks when the FSM sets the UNLOCK output signal to 1, which it does whenever the last N button presses correspond to the N-digit combination.

  1. Unfortunately the design notes for the P3 are incomplete. Using the specification above and clues gleaned from the partially completed diagrams below fill in the information that is missing from the state transition diagram with its accompanying truth table. When done

    • each state in the transition diagram should be assigned a 2-bit state name S1S0 (note that in this design the state name is not derived from the combination that opens the lock),
    • the arcs leaving each state should be mutually exclusive and collectively exhaustive,
    • the value for UNLOCK should be specified for each state, and
    • the truth table should be completed.

  1. What is the combination for the lock?

Problem 3. Construct a "divisible-by-3" FSM that accepts a binary number entered one bit at a time, most significant bit first, and indicates with a light if the number entered so far is divisible by 3.

  1. Draw a state transition diagram for your FSM indicating the initial state and for which states the light should be turned on. Hint: the FSM has 3 states.
  1. Construct a truth table for the FSM logic. Inputs include the state bits and the next bit of the number; outputs include the next state bits and the control for the light.
  1. Draw a logic schematic for the FSM.

Problem 4.

  1. An FSM, M, is constructed by connecting the output of a 3-state FSM to the inputs of an 9-state FSM. M is then reimplemented using a state register with the minimum number of bits. What is the maximum number of bits that may be needed to reimplement M?
  1. You connect M N-state FSMs, each have 1 input and 1 output, in series. What's an upper bound on the number of states in the resulting FSM?

Problem 5. Ben Bitdiddle has designed an electronic lock with three buttons: "reset", "0" and "1". He has provided the following state transition diagram showing how the lock responds to a sequence of inputs.

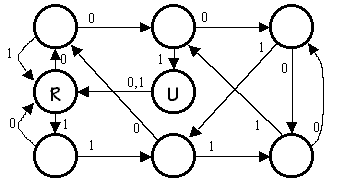
The lock makes a transition from its current state to a new state whenever one of the three buttons is pressed and released. It ignores its inputs if more than one button is pressed. Pressing "reset" returns the lock to the state marked "R" in the diagram (arcs showing the transitions to the reset state have been omitted from the diagram to make it easier to read). Pressing "0" or "1" will cause the lock to follow the appropriately labeled transition from its current state. The lock opens if it reaches the state marked "U".

  1. After pressing the "reset" button what is the length of the shortest sequence of button presses that will open the lock?
  1. After pressing the "reset" button what is the length of the longest sequence of button presses that will cause the lock to open after the last button in the sequence is pressed but not open any earlier in the sequence?
  1. After much use, the "reset" button breaks. Is it still possible to open the lock using only the "0" and "1" buttons assuming you know nothing about the lock's state (except that its locked!) when you start?
  1. Suppose Ben wanted to design a lock that required exactly 10 button presses to open after pressing "reset". Not counting the "reset" and "unlock" states, what is the minimum number of state his FSM would need need?

Problem 6. Stimulated by the idea of FSMs, you have decided to cover MIT's steep tuition costs by selling simple digital locks based on the following six-state FSM:

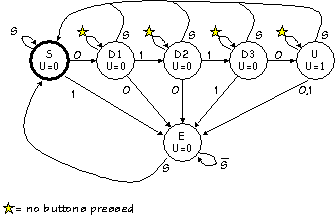
Recall that this design has three buttons labeled "0", "1", and "Start", and generates an unlock signal U=1 when the user presses Start followed by the sequence 0,1,1,0.

Unfortunately your partner, Mark Ting, insists that the design is way too complex for normal users to understand. After asking you to help figure out how to make his watch stop beeping ("I never could figure out how to operate this damned thing"), Mark questions the need for a Start button. If 0110 is the combination, he argues, why can't I just walk up and enter 0,1,1,0 and have the lock open? After some reflection, you conclude that he may have a point.

  1. Design a FSM whose inputs are simply "0" and "1" buttons, whose output is the U (unlock) signal, and which has the property that U=1 if and only if the last four button presses correspond to the sequence 0,1,1,0. Show the state transition diagram corresponding to your design. [HINT: 5 states are sufficient].
  1. Is it possible that an equivalent FSM might be implemented in fewer than 5 states? Explain.
  1. The flip flops used to hold your FSM state contain random values when power is first applied to your lock. Does this constrain your handling of unused states? Explain.
  1. In a table give the contents of a ROM that might be used in an implementation of your design. Completely specify the ROM contents, including those corresponding to unused states.

Problem 7. A possible implementation of a finite state machine with one input and one output is shown below.

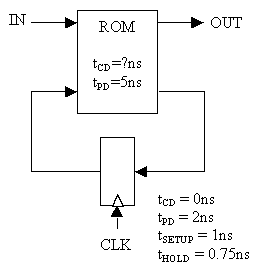
  1. If the register is N bits wide, what is the appropriate size of the ROM? Give the number of locations and the number of bits in each location.
  1. If the register is N bits wide, what is the least upper bound on the number of states in a FSM implemented using this circuit?

Problem 8. Ben Bitdiddle has designed an electronic lock with three buttons: "Breset", "B0" and "B1". He has provided the following circuit diagram showing how the lock is implemented from a ROM and 3 flip-flops.

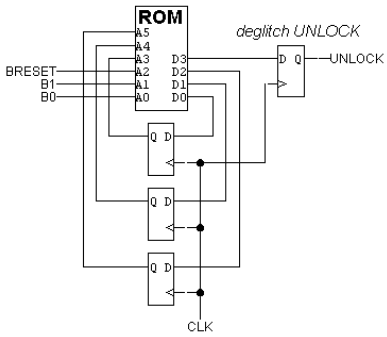
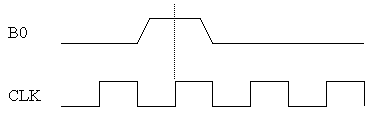
The button circuitry converts each button press into a single pulse guaranteed to be stable the required amount of time before and after the rising edge of the clock. For example, pressing "B0" once produces the following waveform:

In answering the questions below, assume that the value of the UNLOCK output is only a function of the current state.

  1. What is the total number of bits in the ROM?
  1. The timing specifications for components are:

      ROM: tCD=3ns, tPD=11ns
      D flip-flop: tCD=2ns, tPD=4ns, tS=3ns, tH=3ns

    How long before the rising edge of CLK must the button circuitry guarantee that the button signals are stable?

  1. Assume that all combinations start with pressing the "Breset" button. Ben wants to program the lock with the longest possible combination. Not counting the "Breset" button press, what is the longest combination Ben can achieve?
  1. If the lock is programmed not to change state if no buttons are pressed, what is the next state field of ROM location 48 (i.e., the location corresponding to A5,A4,A3,A2,A1,A0 = 110000)?
  1. The following table shows one possible contents of the first 32 locations of the ROM; assume that all other locations have the value "0010". The location is listed as A5,A4,A3,A2,A1,A0, the data is listed as D3,D2,D1,D0.

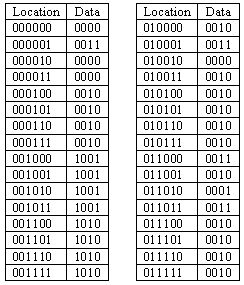    If the lock is programmed with this ROM data, what happens when "B0" and "B1" are pressed at the same time? Assume that "Breset" is not pressed.

  1. If the lock is programmed with this ROM data, what is the shortest combination that opens the lock after "Breset" has been pressed?
  1. Suppose that the "Breset" button breaks while the lock is locked. Is it still possible to open the lock using a predetermined sequence of presses of the "B0" and "B1" buttons? Assume you know nothing about the lock's state (except that it's locked!) when you start.

Problem 9. Consider the following FSM state transition diagram:

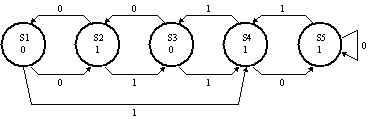
Let's see if there is an equivalent state machine with fewer states by checking to see if any states in the diagram above are equivalent. Two states are equivalent if (1) they have identical outputs and (2) for each possible combination of inputs they transition to equivalent states.

  1. Start by filling in a "compatibility table" like the one shown below. Place an "X" in square (SI,SJ) if SI produces a different output from SJ.

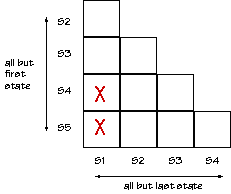
  1. For each non-X square (SI,SJ) write in pairs of states that have to be equivalent in order for SI and SJ to be equivalent. For example, for S2 to be equivalent to S5, then S1 (where S2 goes with a "0" input) has to be equivalent to S5 (where S5 goes with a "0" input).

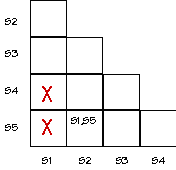
  1. Finally, look at an entry (SI,SJ). If entry is "SM,SN" and if (SM,SN) has an "X", put an "X" in square (SI,SJ). Repeat until no more squares can be X'ed out. The remaining squares indicate equivalent states. Show the final state (no pun intended) of your compatibility table.
  1. Draw the state transition diagram for the simplified FSM.