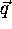should be
be separated by
Because we estimated the Fourier transform by making the x-space
function periodic, it also means that the reciprocal space amplitude
function will be discrete, and harmonically related. Using this
information, we can determine that the values for 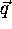should be
be separated by
where N is the number of
points in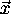 
, and is chosen to be odd to simplify matters.
Furthermore, the maximum (most positive) and minimum (most negative)
values of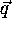 
should be
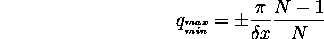
Note, to take into account larger values of q (``higher
frequencies''), we should decreas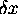e 
(``increase the sampling
frequency''). To decrease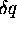 
(without increasing 
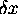we
should make our maximum value of x larger, and keep N the same.
In 6.011 you will learn more about the numerical issues concerning the Discrete Fourier Transform. You will also learn how to accelerate its computation by a method known as the Fast Fourier Transform (FFT).